2022-2023學年湖北省武漢市華中科大附中等七校聯考九年級（上）月考數學試卷（10月份）

一、選擇題（共10小題，每小題3分，共30分）

• 1．若關于x的方程（a-1）x²+4x-4=0是一元二次方程，則a的取值范圍為（　　）

  A．a≠1

  B．a＞1

  C．a＜1

  D．a≠0
  組卷：93引用：3難度：0.8

  解析

• 2．方程x²+2x=5（x-2）的二次項系數、一次項系數、常數項分別為（　　）

  A．1，-3，2

  B．1.7，-10

  C．1，-5，12

  D．1，-3，10
  組卷：70引用：3難度：0.8

  解析

• 3．不解方程，判斷方程x²+2x-1=0的根的情況是（　　）

  A．有兩個相等的實根	B．有兩個不相等的實數根
  C．無實數根	D．無法確定
  組卷：84引用：11難度：0.9

  解析

• 4．拋物線y=-2（x-1）²-1可由拋物線y=-2x²平移得到，則平移的方式是（　　）

  A．向右平移1個單位長度，再向上平移1個單位長度

  B．向左平移1個單位長度，再向上平移1個單位長度

  C．向右平移1個單位長度，再向下平移1個單位長度

  D．向左平移1個單位長度，再向下平移1個單位長度
  組卷：96引用：1難度：0.8

  解析

• 5．由二次函數y=2（x-3）²+1可知（　　）

  A．圖象開口向下

  B．圖象向左平移1個單位得到y=2（x-2）2+1

  C．圖象的對稱軸為直線x=-3

  D．當x＜3時，y隨x的增大而增大
  組卷：204引用：6難度：0.7

  解析

• 6．如圖，要為一幅長29cm,寬22cm的照片外部配一個相框，要求相框的四條邊寬度相等，且相框所占面積為照片面積的四分之一，相框邊的寬度應是多少厘米？設相框邊的寬度為x cm,則可列方程為（　　）

  A．（29+2x）（22+2x）-29×22× 3 4

  B．（29-2x）（22-2x）-29×22× 3 4

  C．（29+2x）（22+2x）=29×22× 5 4

  D．（29-2x）（22-2x）=29×22× 5 4
  組卷：220引用：3難度：0.7

  解析

• 7．拋物線y=2（x-1）²+c過（-2，y₁），（0，y₂），（

  5

  2

  ，y₃）三點，則y₁，y₂，y₃大小關系是（　　）

  A．y2＞y3＞y1

  B．y1＞y2＞y3

  C．y2＞y1＞y3

  D．y1＞y3＞y2
  組卷：1016引用：15難度：0.6

  解析

• 8．若a≠b,且a²-4a+1=0，b²-4b+1=0，則

  1

  1

  +

  a

  2

  +

  1

  1

  +

  b

  2

  的值為（　　）

  A． 1 4

  B．1

  C．4

  D．3
  組卷：1133引用：10難度：0.8

  解析

三、解答題（共8小題，共72分）

• 23．問題背景
  （1）如圖1，已知△ABC是等邊三角形，∠ADB=60°，過C點作CM⊥BD于M點，過C點作CN⊥AD于N點，求證：DC平分∠ADM．
  嘗試應用
  （2）如圖2，已知在等腰直角△ABC中，AB=AC，∠BAC=90°，E是BC中點，在△ABC內部作∠ADC=90°，且∠ADB=135°，連接DE，求證：BD²+DE²=BE²．
  拓展創新
  （3）如圖3，已知△ADF中，∠FAD=75°，AD=2，延長FA至B點，∠BAC=52.5°，H是DF的中點，過H點作DF的垂線交AC的反向延長線于E點，連接ED，∠EDA=7.5°，請直接寫出DF的長度．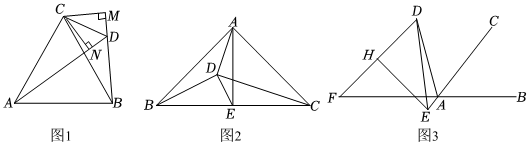
  
  組卷：107引用：1難度：0.1

  解析

• 24．在平面直角坐標系中，拋物線y=x²+（k+1）x+k（k為常數）與x軸交于A、B兩點（點A在點B的左側），與y軸交于點C．
  （1）當k=-3時，直接寫出A，B，C三點的坐標；
  （2）在（1）的條件下，如圖1，連接BC，點E是第四象限內拋物線上的動點，過點E作EF⊥BC于點F，EG∥x軸交直線BC于點G，求△EFG面積的最大值；
  （3）如圖2，當k＜0（k≠-1）時，在直線l：y=kx+1上是否存在點Q，使得△OQB為直角三角形且這樣的Q點有且只有3個？若存在，請求出此時k的值，并求出所有的Q點坐標；若不存在，請說明理由．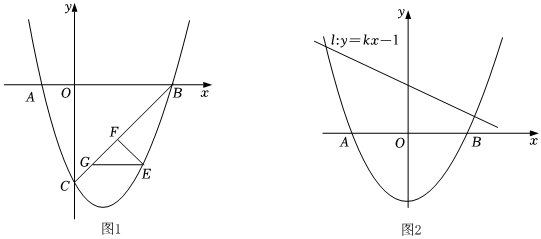
  
  組卷：234引用：1難度：0.3

  解析