2011年第十六屆“華羅庚金杯”少年數學邀請賽總決賽試卷（小學組第1試）

一、填空題（共3題，每題10分）

• 1．計算：

  3

  4

  +

  5

  36

  +

  7

  144

  +

  9

  400

  +

  11

  900

  +

  13

  1764

  +

  15

  3136

  =

  ．
  組卷：169引用：2難度：0.9

  解析

• 2．如圖所示，正方形ABCD的面積為12，AE=ED，且EF=2FC，那么△ABF的面積是

  ．
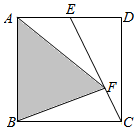  組卷：121引用：2難度：0.5

  解析

二、解答題（共3題，每題10分，寫出解答過程）

• 5．紙板上寫著100、200、400三個自然數，再寫上兩個自然數，然后從這五個數中選出若干個（至少兩個）做只有加、減法的四則運算，在一個四則運算式子中，選出的數只能出現一次，經過所有這樣的運算，可以得到k個不同的非零自然數．那么k最大是多少？
  組卷：53引用：2難度：0.3

  解析

• 6．將1，2，3，4，5，6，7，8，9填入如圖的圓圈中，每個圓圈恰填一個數，滿足下列條件：
  （1）正三角形各邊上的數之和相等；
  （2）正三角形各邊上的數之平方和除以3的余數相等．
  問：有多少種不同的填入方法？
  （注意，經過旋轉和軸對稱反射，排列一致的，視為同一種填法）
  組卷：98引用：1難度：0.1

  解析