2010年數(shù)學(xué)奧林匹克模擬試卷（18）

一、選擇題（共6小題，每小題4分，滿分24分）

• 1．設(shè)六位數(shù)N=

  ?

  x

  1527

  y

  （其中x,y分別表示十萬(wàn)位數(shù)及個(gè)位上的數(shù)字），又N是4的倍數(shù)，且N被11除余5，那么x+y等于（　　）

  A．8

  B．9

  C．11

  D．8或11
  組卷：123引用：2難度：0.5

  解析

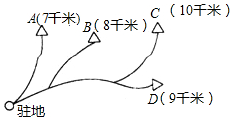• 2．某校學(xué)生打算在星期天去登山，他們計(jì)劃上午8：30出發(fā)，盡可能去登圖中最遠(yuǎn)的山，在山頂開展1個(gè)半小時(shí)的文娛活動(dòng)，于下午3點(diǎn)以前必須返回駐地．如果去時(shí)平均速度為3.2千米/小時(shí)，返回時(shí)平均速度為4.5千米/小時(shí)，則能登上的最遠(yuǎn)的那個(gè)山頂是（　　）

  A．A

  B．B

  C．C

  D．D
  組卷：106引用：1難度：0.9

  解析

• 3．已知等腰三角形ABC中，AB=AC，BC=4，內(nèi)切圓半徑為1，則腰長(zhǎng)為（　　）

  A． 10 3

  B． 11 3

  C．4

  D． 13 3
  組卷：74引用：1難度：0.9

  解析

• 4．設(shè)x≥0，y≥0，2x+y=6，則P=4x²+3xy+y²-6x-3y（　　）

  A．有最大值18，無(wú)最小值	B．無(wú)最大值，有最小值 27 2
  C．有最大值18，最小值 27 2	D．既無(wú)最大值又無(wú)最小值
  組卷：263引用：1難度：0.9

  解析

三、解答題（共3小題，滿分56分）

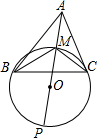• 12．已知M是△ABC內(nèi)一點(diǎn)，且∠BMC=90°+

  1

  2

  ∠BAC，又直線經(jīng)過△BMC的外接圓的圓心O，試證明：點(diǎn)M是△ABC內(nèi)切圓的圓心．
  組卷：174引用：1難度：0.3

  解析

• 13．邊長(zhǎng)為1的正三角形ABC的中心O，以O(shè)為圓心，在正三角形內(nèi)畫一個(gè)圓，（⊙O），再作⊙O₁，⊙O₂，⊙O₃，分別與正三角形的兩邊及⊙O都相切，試求，這四個(gè)面積總和的最大值與最小值，并指出面積總和取最值時(shí)對(duì)應(yīng)的⊙O的半徑．
  組卷：37引用：1難度：0.5

  解析