當前位置：試卷中心 > 試卷詳情

2021-2022學年山西省忻州市高二（下）期末數學試卷

發布：2024/5/3 8:0:9

1．命題“?x∈（0，+∞），x²-2x+lnx＜0”的否定為（　　）
A．?x∈（0，+∞），x²-2x+lnx＞0
B．?x∈（0，+∞），x²-2x+lnx≥0
C．?x∈（0，+∞），x²-2x+lnx＞0
D．?x∈（0，+∞），x²-2x+lnx≥0
組卷：10引用：2難度：0.8
解析
2．隨機變量X服從正態分布N（μ，σ²），且P（X＞-1）=P（X＜5），則下列說法一定正確的是（　　）
A．μ=3 B．μ=2 C．σ=3 D．σ=2
組卷：19引用：4難度：0.8
解析
3．已知集合
A
=
{
x
|
2
x
-
3
＞
1
}
，
B
=
{
x
|
y
=
-
x
-
1
}
，則A∪B=（　　）
A．（-∞，-1]∪（2，+∞） B．（-∞，-1）∪（2，+∞）
C．[-1，2） D．（-1，2）
組卷：195引用：2難度：0.8
解析
4．已知橢圓C：
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）的左、右焦點分別為F₁，F₂，P為橢圓C上一點，若△PF₁F₂的周長為18，長半軸長為5，則橢圓C的離心率為（　　）
A．
3
4
B．
4
5
C．
2
3
D．
2
2
5
組卷：441引用：6難度：0.7
解析
5．函數f（x）=（e^x-e^-x）x²的圖象大致為（　　）
A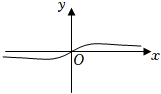． B．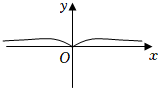
C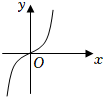． D．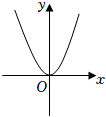
組卷：131引用：4難度：0.8
解析
6．拋物線y²=4x上一點P到原點的距離為
4
2
，則P到焦點的距離為（　　）
A．4 B．5 C．6 D．7
組卷：10引用：2難度：0.7
解析
7．計算2¹⁰+2⁹×3+2⁸×3²+…+3¹⁰=（　　）
A．3¹¹-2¹¹ B．3¹¹+2¹¹ C．3¹¹-1 D．2¹¹-1
組卷：132引用：3難度：0.7
解析

21．已知雙曲線
E
：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的右焦點為F₂，點F₂到E的一條漸近線的距離為
2
，過點F₂的直線與E相交于A，B兩點．當AB⊥x軸時，
|
AB
|
=
2
2
．
（1）求E的方程；
（2）若
M
（
3
2
，
0
）
，N是直線x=1上一點，當B，M，N三點共線時，判斷直線AN的斜率是否為定值．若是定值，求出該定值；若不是定值，說明理由．
組卷：83引用：3難度：0.4
解析
22．已知函數f（x）=（x-2）e^x-k（x-lnx）．
（1）當k=0時，求f（x）的極值；
（2）證明：當k＞e,x＞1時，f（x）＞-k²．
組卷：3引用：2難度：0.3
解析

A．（-∞，-1]∪（2，+∞）	B．（-∞，-1）∪（2，+∞）
C．[-1，2）	D．（-1，2）

A．	B．
C．	D．

1．命題“?x∈（0，+∞），x2-2x+lnx＜0”的否定為（ ）