2022-2023學年新疆和田地區民豐縣高二（上）期中數學試卷

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知曲線C的方程為

  x

  2

  a

  +

  y

  2

  b

  =1，則“a＞b”是“曲線C為焦點在x軸上的橢圓”的（　　）

  A．充分必要條件	B．充分不必要條件
  C．必要不充分條件	D．既不充分也不必要條件
  組卷：1683引用：6難度：0.9

  解析

• 2．已知直線l₁：y=x+2與l₂：2ax+y-1=0垂直，則a=（　　）

  A． 1 2

  B．- 1 2

  C．-1

  D．1
  組卷：126引用：5難度：0.7

  解析

• 3．設F₁，F₂分別是橢圓C：

  x

  2

  12

  +

  y

  2

  m

  =

  1

  的左、右兩個焦點，若C上存在點P滿足∠F₁PF₂=120°，則m的取值范圍是（　　）

  A．[3，+∞）

  B．[3，12）

  C．（0，6]

  D．（0，3]
  組卷：87引用：2難度：0.6

  解析

• 4．已知直線l的方程為xsinα+

  3

  y-1=0，α∈R，則直線l的傾斜角范圍（　　）

  A．（0， π 3 ]∪[ 2 π 3 ，π）	B．[0， π 6 ]∪[ 5 π 6 ，π）
  C．[0， π 6 ）∪（ 5 π 6 ，π）	D．[0， π 3 ]∪[ 2 π 3 ，π）
  組卷：529引用：6難度：0.7

  解析

• 5．對于任意實數a,點P（a,2-a）與圓C：x²+y²=1的位置關系的所有可能是（　　）

  A．都在圓內	B．都在圓外
  C．在圓上、圓外	D．在圓上、圓內、圓外
  組卷：150引用：6難度：0.9

  解析

• 6．已知直線l的方程為

  xsinα

  +

  3

  y

  -

  1

  =

  0

  ，α∈R，則直線l的傾斜角范圍（　　）

  A． （ 0 ， π 3 ] ∪ [ 2 π 3 ， π ）	B． [ 0 ， π 6 ] ∪ [ 5 π 6 ， π ）
  C． [ 0 ， π 6 ） ∪ （ 5 π 6 ， π ）	D． [ 0 ， π 3 ] ∪ [ 2 π 3 ， π ）
  組卷：38引用：1難度：0.8

  解析

• 7．圓

  C

  1

  ：

  x

  2

  +

  y

  2

  =

  1

  與圓

  C

  2

  ：

  （

  x

  -

  3

  ）

  2

  +

  （

  y

  -

  4

  ）

  2

  =

  25

  -

  m

  （m＜25）外切，則m=（　　）

  A．21

  B．19

  C．9

  D．-11
  組卷：41引用：4難度：0.9

  解析

四、解答題；本題共6個小題，共70分．解答應寫出文字說明，證明過程或演算步驟．

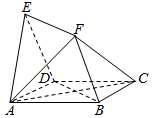• 21．如圖，四邊形ABCD與BDEF均為菱形，FA=FC，且∠DAB=∠DBF=60°．
  （1）求證：AC⊥平面BDEF；
  （2）若菱形BDEF邊長為2，求三棱錐E-BCD的體積．
  組卷：301引用：4難度：0.4

  解析

• 22．已知橢圓M：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的離心率為

  3

  2

  ，且橢圓上一點P的坐標為（

  2

  ，

  2

  2

  ）．
  （1）求橢圓M的方程；
  （2）設直線l與橢圓M交于A，B兩點，且以線段AB為直徑的圓過橢圓的右頂點C，求△ABC面積的最大值．
  組卷：973引用：4難度：0.4

  解析