2017-2018學(xué)年湖北省武漢市洪山區(qū)華中師大一附中九年級（上）起點(diǎn)考數(shù)學(xué)試卷

一、選擇題（共10小題，每小題3分，共30分）

• 1．一元二次方程2x²-6x=4的二次項(xiàng)系數(shù)，一次項(xiàng)系數(shù)和常數(shù)項(xiàng)之比正確的是（　　）

  A．2：（-6）：4	B．1：（-3）：（-2）
  C．1：3：2	D．1：3：（-2）
  組卷：54引用：4難度：0.9

  解析

• 2．方程x²=5x的解為（　　）

  A．x1=0，x2=-5

  B．x=5

  C．x1=0，x2=5

  D．x=0
  組卷：96引用：4難度：0.7

  解析

• 3．用配方法解方程3x²-6x+1=0，則方程可變形為（　　）

  A．（x-3）2= 1 3

  B．3（x-1）2= 1 3

  C．（3x-1）2=1

  D．（x-1）2= 2 3
  組卷：1488引用：91難度：0.9

  解析

• 4．已知方程x²+bx+a=0有一個(gè)根是-a（a≠0），則下列代數(shù)式的值恒為常數(shù)的是（　　）

  A．a(chǎn)b

  B． a b

  C．a(chǎn)+b

  D．a(chǎn)-b
  組卷：1082引用：71難度：0.7

  解析

• 5．已知一元二次方程2x²-3x-6=0有兩個(gè)實(shí)數(shù)根x₁、x₂，直線l經(jīng)過點(diǎn)A（x₁+x₂，0）、B（0，x₁?x₂），則直線l的解析式為（　　）

  A．y=2x-3

  B．y=2x+3

  C．y=-2x-3

  D．y=-2x+3
  組卷：243引用：19難度：0.9

  解析

• 6．某區(qū)為踐行“人人享受教育”的理念，加強(qiáng)了對教師隊(duì)伍的建設(shè)的投入，2012年投入1000萬元，預(yù)計(jì)2013年、2014年共投入2310萬元，設(shè)投入經(jīng)費(fèi)的年平均增長率為x,根據(jù)題意，下面所列方程正確的是（　　）

  A．1000（1+x）2=2310

  B．1000（x2+1）=2310

  C．1000+1000（1+x）+1000（1+x）2=2310

  D．1000（1+x）+1000（1+x）2=2310
  組卷：41引用：3難度：0.9

  解析

• 7．已知二次函數(shù)y=ax²-2ax+1（a＜0）圖象上三點(diǎn)A（-1，y₁）、B（2，y₂）、C（4，y₃），則y₁，y₂，y₃的大小關(guān)系為（　　）

  A．y1＜y2＜y3

  B．y2＜y1＜y3

  C．y1＜y3＜y2

  D．y3＜y1＜y2
  組卷：287引用：2難度：0.6

  解析

• 8．函數(shù)y=ax+1與y=ax²+bx+1（a≠0）的圖象可能是（　　）

  A．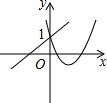

  B．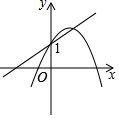

  C．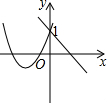

  D．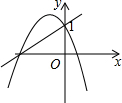
  組卷：1671引用：15難度：0.7

  解析

三、解答題（共8題，共72分）

• 23．交通工程學(xué)理論把在單向道路上行駛的汽車看成連續(xù)的流體，并用流量、速度、密度三個(gè)概念描述車流的基本特征．其中流量q（輛/小時(shí)）指單位時(shí)間內(nèi)通過道路指定斷面的車輛數(shù)；速度v（千米/小時(shí)）指通過道路指定斷面的車輛速度；密度k（輛/千米）指通過道路指定斷面單位長度內(nèi)的車輛數(shù)．
  為配合大數(shù)據(jù)治堵行動，測得某路段流量q與速度v之間關(guān)系的部分?jǐn)?shù)據(jù)如下表：
  

  速度v（千米/小時(shí)）	…	5	10	20	32	40	48	…
  流量q（輛/小時(shí)）	…	550	1000	1600	1792	1600	1152	…

  （1）根據(jù)上表信息，下列三個(gè)函數(shù)關(guān)系式中，刻畫q,v關(guān)系最準(zhǔn)確的是

  （只填上正確答案的序號）
  ①q=90v+100；②q=

  32000

  v

  ；③q=-2v²+120v.
  （2）請利用（1）中選取的函數(shù)關(guān)系式分析，當(dāng)該路段的車流速度為多少時(shí)，流量達(dá)到最大？最大流量是多少？
  （3）已知q,v,k滿足q=vk,請結(jié)合（1）中選取的函數(shù)關(guān)系式繼續(xù)解決下列問題．
  ①市交通運(yùn)行監(jiān)控平臺顯示，當(dāng)12≤v＜18時(shí)道路出現(xiàn)輕度擁堵．試分析當(dāng)車流密度k在什么范圍時(shí)，該路段將出現(xiàn)輕度擁堵；
  ②在理想狀態(tài)下，假設(shè)前后兩車車頭之間的距離d（米）均相等，求流量q最大時(shí)d的值．
  組卷：1643引用：9難度：0.3

  解析

• 24．如圖甲，在平面直角坐標(biāo)系中，A、B的坐標(biāo)分別為（4，0）、（0，3），拋物線

  y

  =

  3

  4

  x

  2

  +

  bx

  +

  c

  經(jīng)過點(diǎn)B，且對稱軸是直線

  x

  =

  -

  5

  2

  ．
  （1）求拋物線對應(yīng)的函數(shù)解析式；
  （2）將圖甲中的△ABO沿x軸向左平移得到△DCE（如圖乙），當(dāng)四邊形ABCD是菱形時(shí)，請說明點(diǎn)C和點(diǎn)D都在該拋物線上．
  （3）在（2）中，若點(diǎn)M是拋物線上的一個(gè)動點(diǎn)（點(diǎn)M不與點(diǎn)C、D重合），通過M作MN∥y軸交直線CD于N，設(shè)點(diǎn)M的橫坐標(biāo)為t,MN的長度為l,求l與t之間的函數(shù)解析式．并求當(dāng)為何值時(shí)，以M、N、C、E為頂點(diǎn)的四邊形是平行四邊形．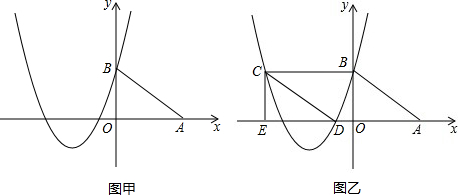
  
  組卷：97引用：4難度：0.5

  解析