2023-2024學(xué)年陜西省咸陽(yáng)市武功縣普集高級(jí)中學(xué)高二（上）期中數(shù)學(xué)試卷

一、單項(xiàng)選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的．

• 1．若直線經(jīng)過(guò)A（1，0），

  B

  （

  4

  ，

  3

  ）

  兩點(diǎn)，則直線AB的傾斜角為（　　）

  A．30°

  B．45°

  C．60°

  D．135°
  組卷：202引用：4難度：0.8

  解析

• 2．設(shè)x,y∈R，向量

  a

  =

  （

  0

  ，

  1

  ，

  z

  ）

  ，

  b

  =

  （

  2

  ，

  y

  ,

  2

  ）

  ，

  c

  =

  （

  -

  3

  ，

  6

  ，-

  3

  ）

  ，且

  a

  ⊥

  c

  ，

  b

  ∥

  c

  ，則

  |

  a

  -

  b

  |

  =（　　）

  A． 29

  B． 2 6

  C．3

  D． 2 2
  組卷：78引用：11難度：0.7

  解析

• 3．在平面直角坐標(biāo)系xOy中，以點(diǎn)（0，1）為圓心且與直線x-y-1=0相切的圓的標(biāo)準(zhǔn)方程為（　　）

  A．x2+（y-1）2=2	B．（x-1）2+y2=1
  C． x 2 + （ y - 1 ） 2 = 2	D．（x-1）2+y2=4
  組卷：423引用：11難度：0.8

  解析

• 4．如圖，在四棱錐P-ABCD中，PA⊥底面ABCD，底面ABCD為正方形，PA=BC，E為CD的中點(diǎn)，F(xiàn)為PC的中點(diǎn)，則異面直線BF與PE所成角的余弦值為（　　）

  A． 2 3 9

  B． 4 3 9

  C． 3 9

  D． 5 3 9
  組卷：227引用：5難度：0.7

  解析

• 5．已知圓C₁的標(biāo)準(zhǔn)方程是（x-4）²+（y-4）²=25，圓C₂：x²+y²-4x+my+3=0關(guān)于直線x+

  3

  y+1=0對(duì)稱，則圓C₁與圓C₂的位置關(guān)系為（　　）

  A．相離

  B．相切

  C．相交

  D．內(nèi)含
  組卷：557引用：6難度：0.8

  解析

• 6．設(shè)橢圓中心在原點(diǎn)，兩焦點(diǎn)F₁，F(xiàn)₂在x軸上，點(diǎn)P在橢圓上．若橢圓的離心率為

  1

  2

  ，△PF₁F₂的周長(zhǎng)為12，則橢圓的標(biāo)準(zhǔn)方程是（　　）

  A． x 2 4 + y 2 3 =1	B． x 2 16 + y 2 12 =1
  C． x 2 3 + y 2 4 =1	D． x 2 12 + y 2 16 =1
  組卷：155引用：3難度：0.9

  解析

• 7．若平面內(nèi)兩條平行線l₁：x+（a-1）y+2=0與l₂：ax+2y+1=0間的距離為

  3

  5

  5

  ，則實(shí)數(shù)a=（　　）

  A．-1

  B．2

  C．-l或2

  D．-2或l
  組卷：48引用：2難度：0.7

  解析

四、解答題：本題共6小題，共70分．第17題10分，其他每題12分，解答應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟．

• 21．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的上頂點(diǎn)與橢圓的左，右頂點(diǎn)連線的斜率之積為-

  1

  4

  ．
  （1）求橢圓C的離心率；
  （2）若直線y=

  1

  2

  （

  x

  +

  1

  ）與橢圓C相交于A，B兩點(diǎn)，|AB|=

  35

  2

  ，求橢圓C的標(biāo)準(zhǔn)方程．
  組卷：118引用：4難度：0.6

  解析

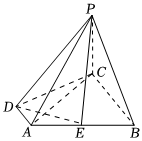• 22．如圖所示，四棱錐P-ABCD中，PC⊥底面ABCD，PC=CD=2，E為AB的中點(diǎn)，底面四邊形ABCD滿足∠ADC=∠DCB=90°，AD=1，BC=3．
  （Ⅰ）證明：DE⊥平面PAC；
  （Ⅱ）求直線PC與平面PDE所成角的正弦值；
  （Ⅲ）求平面PED與平面PEB夾角的余弦值．
  組卷：234引用：3難度：0.5

  解析