2021-2022學年黑龍江省牡丹江第三高級中學高一（下）開學數學試卷

一、單選題（共8小題，每小題5分，共40分）

• 1．cos

  13

  π

  6

  =（　　）

  A． 3 2

  B． - 3 2

  C． 1 2

  D． - 1 2
  組卷：880引用：10難度：0.8

  解析

• 2．已知集合A={x|log₂x＜1}，B={y|y=2^x，x≥0}，則A∩B=（　　）

  A．?

  B．{x|1＜x＜2}

  C．{x|1≤x＜2}

  D．{x|1＜x≤2}
  組卷：229引用：9難度：0.9

  解析

• 3．三個數

  lo

  g

  π

  0

  .

  3

  ，

  3

  π

  ，

  sin

  π

  10

  的大小關系是（　　）

  A． lo g π 0 . 3 ＜ sin π 10 ＜ 3 π	B． lo g π 0 . 3 ＜ 3 π ＜ sin π 10
  C． sin π 10 ＜ lo g π 0 . 3 ＜ 3 π	D． 3 π ＜ lo g π 0 . 3 ＜ sin π 10
  組卷：269引用：13難度：0.7

  解析

• 4．函數f（x）=2^x+3x的零點所在的一個區間是（　　）

  A．（-2，-1）

  B．（0，1）

  C．（-1，0）

  D．（1，2）
  組卷：443引用：10難度：0.9

  解析

• 5．設f（x）=

  2 e x - 1 ， x ＜ 2

  lo g 3 （ x 2 - 1 ） ， x ≥ 2

  ，則f（f（2））的值為（　　）

  A．0

  B．1

  C．2

  D．3
  組卷：90引用：11難度：0.8

  解析

• 6．已知函數f（x）=log

  1

  2

  （x²-4x-5），則函數f（x）的減區間是（　　）

  A．（-∞，2）

  B．（2，+∞）

  C．（5，+∞）

  D．（-∞，-1）
  組卷：5465引用：11難度：0.9

  解析

四、解答題（共4小題，共40分）

• 19．已知cosα=

  1

  7

  ，cos（α-β）=

  13

  14

  ，且0＜β＜α＜

  π

  2

  ，
  （1）求tan2α的值；
  （2）求β．
  組卷：1320引用：37難度：0.3

  解析

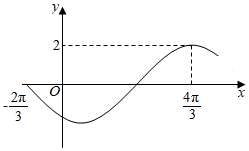• 20．已知函數f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的部分圖象如圖所示．
  （1）求函數f（x）的解析式，并寫出函數f（x）的單調遞增區間；
  （2）將函數f（x）圖象上所有點的橫坐標縮短到原來的

  1

  4

  （縱坐標不變），再將所得的函數圖象上所有點向左平移

  m

  （

  0

  ＜

  m

  ＜

  π

  2

  ）

  個單位長度，得到函數g（x）的圖象．若函數g（x）的圖象關于直線

  x

  =

  5

  π

  12

  對稱，求函數g（x）在區間

  [

  π

  12

  ，

  7

  π

  12

  ]

  上的值域．
  組卷：270引用：7難度：0.6

  解析