2022-2023學年廣東省廣州市六區高二（上）期末數學試卷

一、選擇題：本題共8小題，每小題5分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．直線

  3

  x+y+1=0的傾斜角為（　　）

  A． π 3

  B． 2 π 3

  C． π 6

  D． 5 π 6
  組卷：332引用：62難度：0.9

  解析

• 2．準線方程為x=2的拋物線的標準方程是（　　）

  A．y2=-4x

  B．y2=8x

  C．y2=4x

  D．y2=-8x
  組卷：306引用：8難度：0.9

  解析

• 3．雙曲線

  x

  2

  2

  -

  y

  2

  =1的離心率為（　　）

  A． 6 2

  B． 3 2

  C． 3

  D．3
  組卷：146引用：3難度：0.7

  解析

• 4．經過兩條直線2x+y-8=0和x-2y+1=0的交點，且垂直于直線3x-2y+4=0的直線的方程是（　　）

  A．2x+3y-13=0

  B．2x+3y-12=0

  C．2x-3y=0

  D．2x-3y-5=0
  組卷：176引用：5難度：0.8

  解析

• 5．在三棱柱ABC-A₁B₁C中，M，N分別為A₁C₁，B₁B的中點，若

  MN

  =

  x

  AB

  +

  y

  AC

  +

  z

  A

  A

  1

  ，則（x,y,z）=（　　）

  A．（1，- 1 2 ，- 1 2 ）	B．（1， 1 2 ，- 1 2 ）
  C．（-1， 1 2 ， 1 2 ）	D．（-1， 1 2 ，- 1 2 ）
  組卷：279引用：5難度：0.8

  解析

• 6．動圓P過定點M（0，2），且與圓N：x²+（y+2）²=4相內切，則動圓圓心P的軌跡方程是（　　）

  A． y 2 - x 2 3 = 1 （ y ＜ 0 ）	B． y 2 - x 2 3 = 1
  C． y 2 3 - x 2 = 1 （ y ＜ 0 ）	D． x 2 + y 2 3 = 1
  組卷：223引用：7難度：0.7

  解析

• 7．橢圓

  x

  2

  25

  +

  y

  2

  16

  =

  1

  的一個焦點是F，過原點O作直線（不經過焦點）與橢圓相交于A，B兩點，則△ABF的周長的最小值是（　　）

  A．14

  B．15

  C．18

  D．20
  組卷：213引用：1難度：0.7

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

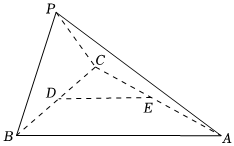• 21．如圖，在三棱錐P-ABC中，∠ABC=90°，AB=BC=4，D，E分別為BC，AC的中點，△PBC為正三角形，平面PBC⊥平面ABC．
  （1）求點B到平面PAC的距離；
  （2）在線段PC上是否存在異于端點的點M，使得平面CPAC和平面MDE夾角的余弦值為

  7

  7

  ？若存在，確定點M的位置；若不存在，說明理由．
  組卷：253引用：6難度：0.4

  解析

• 22．已知橢圓

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  上的點到兩個焦點的距離之和為

  4

  2

  ．短軸的兩個頂點和兩個焦點連接成的四邊形為正方形．
  （1）求橢圓C的方程；
  （2）設點A，B為橢圓C上的兩點，O為坐標原點，

  k

  OA

  ?

  k

  OB

  =

  -

  3

  2

  ，求

  OA

  ?

  OB

  的取值范圍．
  組卷：362引用：3難度：0.4

  解析