2023-2024學年天津五十五中高二（上）期中數學試卷

一、單選題

• 1．若直線過點（3，2），（4，2+

  3

  ），則此直線的傾斜角是（　　）

  A．30°

  B．60°

  C．120°

  D．150°
  組卷：46引用：2難度：0.9

  解析

• 2．過直線x+y+1=0和x-2y+4=0的交點，且與直線x+2y-3=0垂直的直線方程是（　　）

  A．2x-y+3=0

  B．2x-y+5=0

  C．x+2y-4=0

  D．2x-y-3=0
  組卷：518引用：4難度：0.8

  解析

• 3．已知過點P（2，2）的直線與圓（x-1）²+y²=5相切，且與直線ax-y+1=0平行，則a=（　　）

  A．2

  B．1

  C． - 1 2

  D． 1 2
  組卷：1149引用：10難度：0.7

  解析

• 4．已知雙曲線

  x

  2

  a

  2

  -

  y

  2

  9

  =

  1

  的一個焦點在直線x+2y=5上，則雙曲線的漸近線方程為（　　）

  A．y=± 3 4 x

  B．y=± 4 3 x

  C．y=± 2 2 3 x

  D．y=± 3 2 4 x
  組卷：431引用：5難度：0.7

  解析

• 5．如圖，唐金筐寶鈿團花紋金杯出土于西安，這件金杯整體造型具有玲瓏剔透之美，充分體現(xiàn)唐代金銀器制作的高超技藝，是唐代金銀細工的典范之作，該杯柱體部分的軸截面可以近似作雙曲線C的一部分．若C的中心在原點，焦點在x軸上，離心率e=2，且點M（2，

  3

  ）在C上，則雙曲線C的標準方程為（　　）

  A． x 2 - y 2 3 = 1

  B． x 2 3 - y 2 9 = 1

  C． x 2 3 - y 2 = 1

  D． x 2 2 - y 2 3 = 1
  組卷：75引用：3難度：0.9

  解析

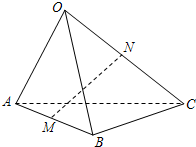• 6．已知三棱錐O-ABC，點M，N分別為AB，OC的中點，且

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  用

  a

  ，

  b

  ，

  c

  表示

  MN

  ，則

  MN

  等于（　　）

  A． 1 2 （ b + c - a ）

  B． 1 2 （ a + b + c ）

  C． 1 2 （ a - b + c ）

  D． 1 2 （ c - a - b ）
  組卷：1475引用：13難度：0.7

  解析

三、解答題

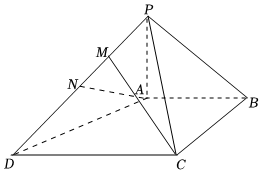• 19．如圖，在四棱錐P-ABCD中，PA⊥平面ABCD，AB∥CD，且CD=2，AB=1，

  BC

  =

  2

  2

  ，

  PA

  =

  1

  ，

  AB

  ⊥

  BC

  ，

  N

  為PD的中點．
  （1）求平面PAD與平面PBC所成銳二面角的余弦值；
  （2）求點N到直線BC的距離；
  （3）在線段PD上是否存在一點M，使得直線CM與平面PBC所成角的正弦值為

  26

  26

  ，若存在，求出

  DM

  DP

  的值；若不存在，說明理由．
  組卷：299引用：4難度：0.4

  解析

• 20．如圖，已知橢圓

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的左右頂點分別是A，B，焦點F（c,0），其中b=c,設點

  P

  （

  a

  ,

  t

  ）

  （

  t

  ≥

  2

  ）

  ，連接PA交橢圓于點C，坐標原點是O．
  （1）求橢圓的離心率；
  （2）證明：OP⊥BC；
  （3）設三角形ABC的面積為S₁，四邊形OBPC的面積為S₂，若

  S

  2

  S

  1

  的最小值為1，求橢圓的標準方程．
  組卷：132引用：1難度：0.5

  解析