2022-2023學年江蘇省連云港市高一（上）調研數學試卷（五）

一、選擇題：本題共8小題，每小題5分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知集合A={-2，-1，0，1，2}，B={x|（x-1）（x+2）＜0}，則A∩B=（　　）

  A．{-1，0}

  B．{0，1}

  C．{-1，0，1}

  D．{0，1，2}
  組卷：4353引用：96難度：0.9

  解析

• 2．命題“?x∈R，|x|+x²≥0”的否定是（　　）

  A．?x∈R，|x|+x2＜0	B．?x∈R，|x|+x2≤0
  C．?x0∈R，|x0|+x02＜0	D．?x0∈R，|x0|+x02≥0
  組卷：1900引用：75難度：0.9

  解析

• 3．已知a=

  2

  1

  3

  ，b=（

  1

  3

  ）²，c=log₂

  1

  2

  ，則（　　）

  A．c＜a＜b

  B．b＜a＜c

  C．c＜b＜a

  D．b＜c＜a
  組卷：208引用：5難度：0.8

  解析

• 4．設集合M={x|0＜x≤3}，N={x|0＜x≤2}，那么“a∈M”是“a∈N”的（　　）

  A．充分而不必要條件	B．必要而不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：426引用：55難度：0.9

  解析

• 5．函數y=lnx²的部分圖象可能是（　　）

  A．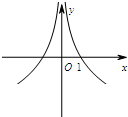

  B．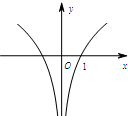

  C．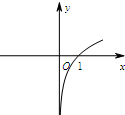

  D．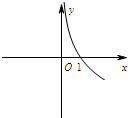
  組卷：90引用：7難度：0.5

  解析

• 6．為了得到函數

  y

  =

  sin

  （

  2

  x

  +

  π

  3

  ）

  的圖象，只要將y=sinx（x∈R）的圖象上所有的點（　　）

  A．向左平移 π 3 個單位長度，再把所得各點的橫坐標縮短到原來的 1 2 ，縱坐標不變

  B．向左平移 π 3 個單位長度，再把所得各點的橫坐標伸長到原來的2倍，縱坐標不變

  C．向左平移 π 6 個單位長度，再把所得各點的橫坐標縮短到原來的 1 2 ，縱坐標不變

  D．向左平移 π 6 個單位長度，再把所得各點的橫坐標伸長到原來的2倍，縱坐標不變
  組卷：199引用：13難度：0.9

  解析

• 7．已知函數f（x）=

  3 x （ x ≤ 0 ）

  log 2 x （ x ＞ 0 ）

  ，那么f[f（

  1

  8

  ）]的值為（　　）

  A．27

  B． 1 27

  C．-27

  D．- 1 27
  組卷：67引用：21難度：0.9

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

• 21．已知二次函數f（x）滿足f（x+1）-f（x）=2x,且f（0）=1．
  （1）求f（x）的解析式；
  （2）設函數g（x）=f（2x-a）（a∈R），x∈[-1，1]，求g（x）的最大值h（a），并求h（a）的最小值．
  組卷：125引用：4難度：0.6

  解析

• 22．若定義在R上的函數f（x）滿足：?x₁，x₂∈R，都有f（x₁+x₂）=f（x₁）+f（x₂）+1成立，且當x＞0時，f（x）＞-1．
  （1）求證：f（x）+1為奇函數；
  （2）求證：f（x）為R上的增函數；
  （3）若f（1）=1，且?x≥0，?y≥0，f[x²-m（2xy+y²）+4m²y²+4]≥7恒成立，求實數m的取值范圍．
  組卷：104引用：2難度：0.5

  解析