《第1章 三角函數》2011年單元測試卷（廣東省深圳外國語學校）

一、選擇題（本大題共12小題，每小題4分，共48分）

• 1．集合{α|kπ+

  π

  4

  ≤α≤kπ+

  π

  2

  ，k∈Z}中的角所表示的范圍（陰影部分）是（　　）

  A．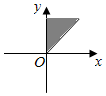

  B．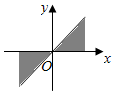

  C．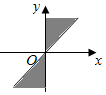

  D．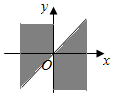
  組卷：5674引用：49難度：0.9

  解析

• 2．已知角α的終邊經過點P（-4m,3m）（m≠0），則2sinα+cosα的值是（　　）

  A．1或-1

  B． 2 5 或- 2 5

  C．1或- 2 5

  D．-1或 2 5
  組卷：2522引用：34難度：0.9

  解析

• 3．已知f（cosx）=cos3x,則f（sinx）等于（　　）

  A．-sin3x

  B．-cos3x

  C．cos3x

  D．sin3x
  組卷：37引用：7難度：0.9

  解析

• 4．已知sinα＞sinβ，那么下列命題成立的是（　　）

  A．若α、β是第一象限角，則cosα＞cosβ

  B．若α、β是第二象限角，則tanα＞tanβ

  C．若α、β是第三象限角，則cosα＞cosβ

  D．若α、β是第四象限角，則tanα＞tanβ
  組卷：1900引用：28難度：0.9

  解析

• 5．若要得到函數y=sin（2x-

  π

  4

  ）的圖象，可以把函數y=sin2x的圖象（　　）

  A．向右平移 π 8 個單位	B．向左平移 π 8 個單位
  C．向右平移 π 4 個單位	D．向左平移 π 4 個單位
  組卷：247引用：62難度：0.9

  解析

• 6．已知α是三角形的一個內角且sin（π-α）-cos（π+α）=

  2

  3

  ，則此三角形是（　　）

  A．銳角三角形

  B．直角三角形

  C．鈍角三角形

  D．等腰三角形
  組卷：47引用：3難度：0.7

  解析

• 7．若|sinθ|=

  1

  5

  ，

  9

  π

  2

  ＜θ＜5π，則tanθ等于（　　）

  A． 6 12

  B．- 2 6

  C． - 6 12

  D． 2 6
  組卷：91引用：1難度：0.9

  解析

• 8．下列函數中，最小正周期為π，且圖象關于直線

  x

  =

  π

  3

  對稱的是（　　）

  A． y = sin （ 2 x + π 6 ）	B． y = sin （ x 2 + π 3 ）
  C． y = sin （ 2 x - π 3 ）	D． y = sin （ 2 x - π 6 ）
  組卷：221引用：49難度：0.9

  解析

三、解答題（本大題62分）

• 25．已知函數f（x）=

  sinx （ sinx ≥ cosx ）

  cosx （ cosx ＞ sinx ）

  
  （1）畫出f（x）的圖象，并寫出其單調區間、最大值、最小值；
  （2）判斷f（x）是否為周期函數．如果是，求出最小正周期．
  組卷：150引用：5難度：0.3

  解析

• 26．設關于x的函數y=2cos²x-2acosx-（2a+1）的最小值為f（a），試確定滿足

  f

  （

  a

  ）

  =

  1

  2

  的a的值，并對此時的a值求y的最大值．
  組卷：121引用：20難度：0.3

  解析