2023-2024學年四川省成都市郫都區高三（上）第一次段考數學試卷（文科）

一、選擇題：本大題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．設集合A={1，2，3，4}，B={x|x＞2}，則A∩B=（　　）

  A．{1，2}

  B．{3，4}

  C．{2，3，4}

  D．{1，2，3，4}
  組卷：129引用：11難度：0.9

  解析

• 2．復數z=1-i（i為虛數單位）的虛部為（　　）

  A．1

  B．-1

  C．i

  D．-i
  組卷：144引用：12難度：0.9

  解析

• 3．函數f（x）=2^x+log₂x的零點所在區間是（　　）

  A． （ 0 ， 1 2 ）

  B． （ 1 2 ， 1 ）

  C．（1，2）

  D．（2，3）
  組卷：220引用：10難度：0.7

  解析

• 4．以模型y=ce^kx（c＞0）去擬合一組數據，設z=lny,將其變換后得到線性回歸方程z=2x-1，則原模型中k,c的值分別是（　　）

  A．k=-2，c=e

  B．k=2，c= 1 e

  C．k=-2，c= 1 e

  D．k=2，c=e
  組卷：146引用：4難度：0.7

  解析

• 5．參數方程

  x = 2 + si n 2 θ

  y = - 1 + 2 co s 2 θ

  （θ為參數）化為普通方程是（　　）

  A．2x-y+5=0	B．2x+y-5=0
  C．2x-y+5=0（2≤x≤3）	D．2x+y-5=0（2≤x≤3）
  組卷：76引用：3難度：0.9

  解析

• 6．執行如圖所示的程序，輸出S的值為（　　）
  

  A．-228

  B．-100

  C．-64

  D．-36
  組卷：18引用：3難度：0.9

  解析

• 7．已知函數

  f

  （

  x

  ）

  =

  - x 2 - 2 ax - 5 ， x ≤ 1

  a x ， x ＞ 1

  是R上的增函數，則實數a的取值范圍是（　　）

  A．（-∞，-1]

  B．[-2，-1]

  C．[-2，0]

  D．（-∞，0]
  組卷：1215引用：12難度：0.7

  解析

三、解答題：本大題共6小題，共70分，解答應寫出文字說明，證明過程或推演步驟.

• 21．已知函數

  f

  （

  x

  ）

  =

  1

  2

  x

  2

  +

  alnx

  -

  4

  x

  （

  a

  ＞

  0

  ）

  ．
  （1）當a=3時，試討論函數f（x）的單調性；
  （2）設函數f（x）有兩個極值點x₁，x₂（x₁＜x₂），證明：f（x₁）+f（x₂）＞lna-10．
  組卷：99引用：4難度：0.2

  解析

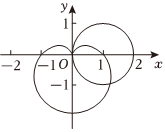• 22．如圖，在平面直角坐標系xOy中，以坐標原點為極點，極軸所在的直線為x軸建立極坐標系，曲線C₁是經過極點且圓心在極軸上的直徑為2的圓，曲線C₂是著名的笛卡爾心形曲線，它的極坐標方程為ρ=1-sinθ（θ∈[0，2π））．
  （1）求曲線C₁的極坐標方程，并求曲線C₁和曲線C₂的交點（異于極點）的極徑；
  （2）若曲線C₃的參數方程為

  x = tcos π 6

  y = tsin π 6

  （t為參數），且曲線C₃和曲線C₂相交于除極點以外的M、N兩點，求線段MN的長度．
  組卷：66引用：4難度：0.5

  解析