2022-2023學年新疆烏魯木齊135中學高二（上）第一次月考數學試卷

一、選擇題（6x8=48）

• 1．在下列命題中：
  ①若向量

  a

  ，

  b

  共線，則向量

  a

  ，

  b

  所在的直線平行；
  ②若向量

  a

  ，

  b

  所在的直線為異面直線，則向量

  a

  ，

  b

  一定不共面；
  ③若三個向量

  a

  ，

  b

  ，

  c

  兩兩共面，則向量

  a

  ，

  b

  ，

  c

  共面；
  ④已知是空間的三個向量

  a

  ，

  b

  ，

  c

  ，則對于空間的任意一個向量

  p

  總存在實數x,y,z使得

  p

  =

  x

  a

  +

  y

  b

  +

  z

  c

  ；
  其中正確的命題的個數是（　　）

  A．0

  B．1

  C．2

  D．3
  組卷：329引用：25難度：0.9

  解析

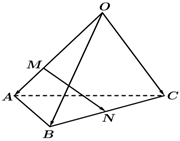• 2．如圖所示，在四面體O-ABC中，

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，點M在OA上，且

  OM

  =2

  MA

  ，N為BC的中點，則

  MN

  =（　　）

  A． 1 2 a - 2 3 b + 1 2 c	B．- 2 3 a + 1 2 b + 1 2 c
  C． 1 2 a + 1 2 b - 2 3 c	D． 2 3 a + 2 3 b - 1 2 c
  組卷：1254引用：41難度：0.9

  解析

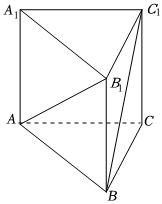• 3．如圖，在正三棱柱ABC-A₁B₁C₁中，若AB=

  2

  B

  B

  1

  ，則AB₁與BC₁所成角的大小為（　　）

  A．60°

  B．90°

  C．105°

  D．75°
  組卷：547引用：20難度：0.7

  解析

• 4．設向量

  a

  、

  b

  、

  c

  不共面，則下列集合可作為空間的一個基底的是（　　）

  A．{ a + b ， b - a ， a }	B．{ a + b ， b - a ， b }
  C．{ a + b ， b - a ， c }	D．{ a + b +c, a + b ， c }
  組卷：344引用：14難度：0.9

  解析

三、解答題（1題14分，12題18分）

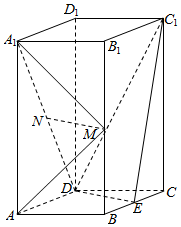• 11．如圖，直四棱柱ABCD-A₁B₁C₁D₁的底面是菱形，AA₁=4，AB=2，∠BAD=60°，E，M，N分別是BC，BB₁，A₁D的中點．
  （1）證明：MN∥平面C₁DE；
  （2）求點C到平面C₁DE的距離．
  組卷：7653引用：34難度：0.4

  解析

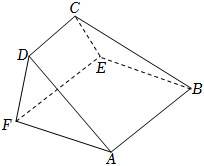• 12．如圖，在以A，B，C，D，E，F為頂點的五面體中，四邊形ABEF為正方形，AF⊥DF，

  AF

  =

  2

  2

  FD

  ，∠DFE=∠CEF=45°．
  （1）求異面直線BC，DF所成角的大小；
  （2）求二面角D-BE-C的余弦值．
  組卷：89引用：3難度：0.5

  解析