人教五四新版九年級(上)中考題單元試卷:第28章 二次函數(30)
發布:2024/4/20 14:35:0
一、填空題(共1小題)
-
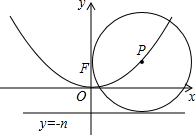 1.如圖,在平面直角坐標系xOy中,若動點P在拋物線y=ax2上,⊙P恒過點F(0,n),且與直線y=-n始終保持相切,則n=(用含a的代數式表示).組卷:2791引用:55難度:0.5
1.如圖,在平面直角坐標系xOy中,若動點P在拋物線y=ax2上,⊙P恒過點F(0,n),且與直線y=-n始終保持相切,則n=(用含a的代數式表示).組卷:2791引用:55難度:0.5
二、解答題(共29小題)
-
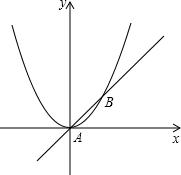 2.如圖,已知直線y=x與拋物線交于A、B兩點.y=12x2
2.如圖,已知直線y=x與拋物線交于A、B兩點.y=12x2
(1)求交點A、B的坐標;
(2)記一次函數y=x的函數值為y1,二次函數的函數值為y2.若y1>y2,求x的取值范圍;y=12x2
(3)在該拋物線上存在幾個點,使得每個點與AB構成的三角形為等腰三角形?并求出不少于3個滿足條件的點P的坐標.組卷:429引用:54難度:0.5 -
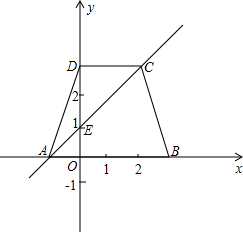 3.如圖,四邊形ABCD是等腰梯形,下底AB在x軸上,點D在y軸上,直線AC與y軸交于點E(0,1),點C的坐標為(2,3).
3.如圖,四邊形ABCD是等腰梯形,下底AB在x軸上,點D在y軸上,直線AC與y軸交于點E(0,1),點C的坐標為(2,3).
(1)求A、D兩點的坐標;
(2)求經過A、D、C三點的拋物線的函數關系式;
(3)在y軸上是否在點P,使△ACP是等腰三角形?若存在,請求出滿足條件的所有點P的坐標;若不存在,請說明理由.組卷:350引用:50難度:0.5 -
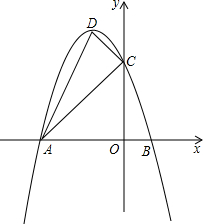 4.如圖,拋物線y=ax2+bx+c的開口向下,與x軸交于點A(-3,0)和點B(1,0).與y軸交于點C,頂點為D.
4.如圖,拋物線y=ax2+bx+c的開口向下,與x軸交于點A(-3,0)和點B(1,0).與y軸交于點C,頂點為D.
(1)求頂點D的坐標.(用含a的代數式表示);
(2)若△ACD的面積為3.
①求拋物線的解析式;
②將拋物線向右平移,使得平移后的拋物線與原拋物線交于點P,且∠PAB=∠DAC,求平移后拋物線的解析式.組卷:930引用:52難度:0.5 -
5.如圖1,已知直線l:y=-x+2與y軸交于點A,拋物線y=(x-1)2+k經過點A,其頂點為B,另一拋物線y=(x-h)2+2-h(h>1)的頂點為D,兩拋物線相交于點C.
(1)求點B的坐標,并說明點D在直線l上的理由;
(2)設交點C的橫坐標為m.
①交點C的縱坐標可以表示為:或,由此進一步探究m關于h的函數關系式;
②如圖2,若∠ACD=90°,求m的值.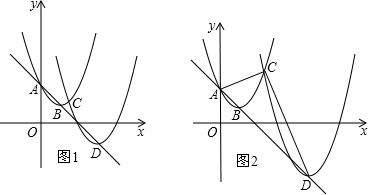 組卷:754引用:51難度:0.5
組卷:754引用:51難度:0.5 -
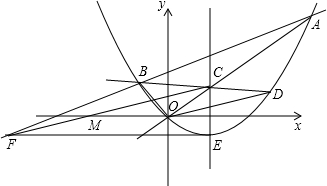 6.如圖,在平面直角坐標系中,直線y=x+12與直線y=x交于點A,點B在直線y=32x+12上,∠BOA=90°.拋物線y=ax2+bx+c過點A,O,B,頂點為點E.32
6.如圖,在平面直角坐標系中,直線y=x+12與直線y=x交于點A,點B在直線y=32x+12上,∠BOA=90°.拋物線y=ax2+bx+c過點A,O,B,頂點為點E.32
(1)求點A,B的坐標;
(2)求拋物線的函數表達式及頂點E的坐標;
(3)設直線y=x與拋物線的對稱軸交于點C,直線BC交拋物線于點D,過點E作FE∥x軸,交直線AB于點F,連接OD,CF,CF交x軸于點M.試判斷OD與CF是否平行,并說明理由.組卷:387引用:51難度:0.5 -
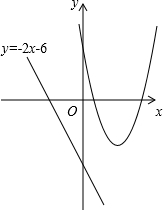 7.已知二次函數y=ax2+bx+c(a≠0)的圖象經過點(1,0),(5,0),(3,-4).
7.已知二次函數y=ax2+bx+c(a≠0)的圖象經過點(1,0),(5,0),(3,-4).
(1)求該二次函數的解析式;
(2)當y>-3,寫出x的取值范圍;
(3)A、B為直線y=-2x-6上兩動點,且距離為2,點C為二次函數圖象上的動點,當點C運動到何處時△ABC的面積最小?求出此時點C的坐標及△ABC面積的最小值.組卷:628引用:51難度:0.5 -
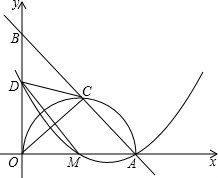 8.如圖,在平面直角坐標系中,直線AB交x軸于點A(5,0),交y軸于點B,AO是⊙M的直徑,其半圓交AB于點C,且AC=3.取BO的中點D,連接CD、MD和OC.
8.如圖,在平面直角坐標系中,直線AB交x軸于點A(5,0),交y軸于點B,AO是⊙M的直徑,其半圓交AB于點C,且AC=3.取BO的中點D,連接CD、MD和OC.
(1)求證:CD是⊙M的切線;
(2)二次函數的圖象經過點D、M、A,其對稱軸上有一動點P,連接PD、PM,求△PDM的周長最小時點P的坐標;
(3)在(2)的條件下,當△PDM的周長最小時,拋物線上是否存在點Q,使S△QAM=S△PDM?若存在,求出點Q的坐標;若不存在,請說明理由.16組卷:471引用:51難度:0.5 -
9.已知△ABC中,邊BC的長與BC邊上的高的和為20.
(1)寫出△ABC的面積y與BC的長x之間的函數關系式,并求出面積為48時BC的長;
(2)當BC多長時,△ABC的面積最大?最大面積是多少?
(3)當△ABC面積最大時,是否存在其周長最小的情形?如果存在,請說出理由,并求出其最小周長;如果不存在,請給予說明.組卷:663引用:52難度:0.5 -
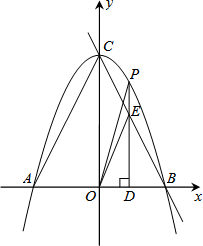 10.如圖,拋物線y=-x2+4與x軸交于A、B兩點,與y軸交于C點,點P是拋物線上的一個動點且在第一象限,過點P作x軸的垂線,垂足為D,交直線BC于點E.
10.如圖,拋物線y=-x2+4與x軸交于A、B兩點,與y軸交于C點,點P是拋物線上的一個動點且在第一象限,過點P作x軸的垂線,垂足為D,交直線BC于點E.
(1)求點A、B、C的坐標和直線BC的解析式;
(2)求△ODE面積的最大值及相應的點E的坐標;
(3)是否存在以點P、O、D為頂點的三角形與△OAC相似?若存在,請求出點P的坐標,若不存在,請說明理由.組卷:536引用:52難度:0.5
二、解答題(共29小題)
-
 29.如圖,已知拋物線與x軸交于A(-1,0),B(3,0)兩點,與y軸交于點C(0,3).
29.如圖,已知拋物線與x軸交于A(-1,0),B(3,0)兩點,與y軸交于點C(0,3).
(1)求拋物線的解析式;
(2)設拋物線的頂點為D,在其對稱軸的右側的拋物線上是否存在點P,使得△PDC是等腰三角形?若存在,求出符合條件的點P的坐標;若不存在,請說明理由;
(3)點M是拋物線上一點,以B,C,D,M為頂點的四邊形是直角梯形,試求出點M的坐標.組卷:1289引用:76難度:0.1 -
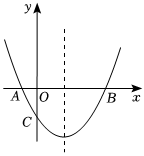 30.如圖,拋物線經過A(-1,0),B(5,0),C(0,-)三點.52
30.如圖,拋物線經過A(-1,0),B(5,0),C(0,-)三點.52
(Ⅰ)求拋物線的解析式;
(Ⅱ)在拋物線的對稱軸上有一點P,使PA+PC的值最小,求點P的坐標.
(Ⅲ)點M為x軸上一動點,在拋物線上是否存在一點N,使以A,C,M,N四點構成的四邊形為平行四邊形?若存在,求點N的坐標;若不存在,請說明理由.組卷:3178引用:92難度:0.3


