2021-2022學年陜西省寶雞市金臺區(qū)高二（下）期末數(shù)學試卷（理科）

一、選擇題：本大題共12個小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．a₁（b₁+b₂）（c₁+c₂+c₃）（d₁+d₂+d₃+d₄）展開后的項數(shù)為（　　）

  A．10

  B．18

  C．24

  D．36
  組卷：351引用：4難度：0.9

  解析

• 2．2022年北京冬奧會的順利召開，引起了大家對冰雪運動的關注．若A，B，C三人在自由式滑雪、花樣滑冰、冰壺和跳臺滑雪這四項運動中任選一項進行體驗，則不同的選法共有（　　）

  A．12種

  B．16種

  C．64種

  D．81種
  組卷：587引用：10難度：0.7

  解析

• 3．下列說法正確的是（　　）

  A．相關關系是一種不確定的關系，回歸分析是對相關關系的分析，因此沒有實際意義

  B．獨立性檢驗對分類變量關系的研究沒有100%的把握，所以獨立性檢驗研究的結果在實際中也沒有多大的實際意義

  C．相關關系可以對變量的發(fā)展趨勢進行預報，這種預報可能是錯誤的

  D．獨立性檢驗如果得出的結論有99%的可信度就意味著這個結論一定是正確的
  組卷：146引用：6難度：0.9

  解析

• 4．投籃測試中，每人投3次，至少投中2次才能通過測試．已知某同學每次投籃投中的概率為0.6，且各次投籃是否投中相互獨立，則該同學通過測試的概率為（　　）

  A．0.648

  B．0.432

  C．0.36

  D．0.312
  組卷：6632引用：49難度：0.9

  解析

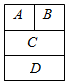• 5．如圖所示，用4種不同的顏色涂入圖中的矩形A，B，C，D中，要求相鄰的矩形涂色不同，則不同的涂法（　　）

  A．72種

  B．48種

  C．24種

  D．12種
  組卷：756引用：14難度：0.9

  解析

• 6．

  （

  1

  +

  2

  x

  ）

  7

  展開式中二項式系數(shù)最大的項是（　　）

  A． 70 2 x 3	B．140x4
  C．70 2 x 3 和140x4	D．140 2 x 5 和140x4
  組卷：85引用：2難度：0.7

  解析

三、解答題：本大題共4小題，共70分.解答應寫出文字說明、證明過程或演算步驟.注意：每題有1分書寫分，要求卷面整潔，書寫規(guī)范，步驟條理清晰.

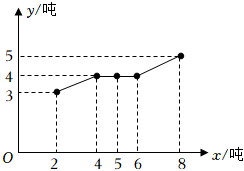• 19．如圖是某采礦廠的污水排放量y（單位：噸）與礦產品年產量x（單位：噸）的折線圖：
  （1）依據(jù)折線圖計算相關系數(shù)r（精確到0.01），并據(jù)此判斷是否可用線性回歸模型擬合y與x的關系？（若|r|＞0.75，則線性相關程度很高，可用線性回歸模型擬合）
  （2）若可用線性回歸模型擬合y與x的關系，請建立y關于x的線性回歸方程，并預測年產量為10噸時的污水排放量．
  相關公式：

  r

  =

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  （

  y

  i

  -

  y

  ）

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  2

  n

  ∑

  i

  =

  1

  （

  y

  i

  -

  y

  ）

  2

  ，參考數(shù)據(jù)：

  0

  .

  3

  ≈

  0

  .

  55

  ，

  0

  .

  9

  ≈

  0

  .

  95

  ．
  回歸方程

  ?

  y

  =

  ?

  b

  x

  +

  ?

  a

  中，

  ?

  b

  =

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  （

  y

  i

  -

  y

  ）

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  2

  ，

  ?

  a

  =

  y

  -

  ?

  b

  x

  ．
  組卷：79引用：6難度：0.9

  解析

• 20．為了響應大學畢業(yè)生自主創(chuàng)業(yè)的號召，小李畢業(yè)后開了水果店，水果店每天以每個5元的價格從農場購進若干西瓜，然后以每個10元的價格出售．如果當天賣不完，剩下的西瓜作贈品處理．
  （1）若水果店一天購進16個西瓜，求當天的利潤y（單位：元）關于當天需求量n（單位：個，n∈N）的函數(shù)解析式；
  （2）水果店記錄了100天西瓜的日需求量（單位：個），整理得下表：
  

  日需求量n	14	15	16	17	18	19	20
  頻數(shù)	10	20	16	16	15	13	10

  以100天記錄的各需求量的頻率作為各需求量發(fā)生的概率．
  ①若水果店一天購進16個西瓜，X表示當天的利潤（單位：元），求X的分布列、數(shù)學期望及方差；
  ②若水果店計劃一天購進16個或17個西瓜，你認為應購進16個還是17個？請說明理由．
  組卷：26引用：1難度：0.5

  解析