2022-2023學年山西省長治市屯留區(qū)九年級（上）期末數(shù)學試卷

一、選擇題（本大題共10個小題.在每小題所給出的四個選項中，只有一項符合題目要求，請選出并在答題卡上將該項涂黑）

• 1．已知拋物線的解析式是

  y

  =

  1

  2

  （

  x

  -

  3

  ）

  2

  -

  4

  ，則該拋物線的頂點坐標是（　　）

  A．（3，4）

  B．（-3，4）

  C．（3，-4）

  D．（-3，-4）
  組卷：132引用：1難度：0.7

  解析

• 2．如圖，點A，B，C在⊙O上，∠BAC=40°，連接OB，OC，則∠BOC的度數(shù)是（　　）

  A．60°

  B．70°

  C．75°

  D．80°
  組卷：184引用：3難度：0.8

  解析

• 3．下列運算中，正確的是（　　）

  A． （ 2 3 - 5 ） （ 2 3 + 5 ） = 1	B． 125 - 45 = 2 5
  C． 28 ÷ （ - 1 2 7 ） = - 8	D． sin 2 60 ° + 2 3 = 5 3 2
  組卷：28引用：1難度：0.7

  解析

• 4．用配方法解方程x²-6x-5=0時，配方后的方程是（　　）

  A．（x-3）2=4

  B．（x-3）2=14

  C．（x-3）2=31

  D．（x+3）2=14
  組卷：135引用：4難度：0.6

  解析

• 5．如圖，直線a,b,c截直線e和f,a∥b∥c,

  AB

  BC

  =

  2

  5

  ，則下列結論中，正確的是（　　）

  A． DF DE = 7 2

  B． EF DE = 3 2

  C． BE CF = 2 5

  D． DF EF = 5 3
  組卷：454引用：3難度：0.7

  解析

• 6．今年2月4日在北京舉辦第24屆冬季奧運會，某校也開展了豐富多彩的冰雪活動．如圖是該校同學參加的冰雪項目學習，小明乘滑雪板沿斜坡滑雪道直線滑行80米，若斜坡滑雪道與水平面的夾角為20°，則他下降的高度為（　　）
  

  A．80sin20°米

  B．80tan20°米

  C． 80 sin 20 ° 米

  D． 80 cos 20 ° 米
  組卷：155引用：1難度：0.6

  解析

• 7．在二次函數(shù)y=ax²+bx+c（a≠0，a,b,c為常數(shù)）中，y與x的部分對應值如下：
  

  x	…	-5	-2.5	-1	0.5	2.5	6	…
  y	…	16	13	4	-5	11	16	…

  根據(jù)表格可知，下列說法中，錯誤的是（　　）

  A．拋物線y=ax2+bx+c開口向上

  B．拋物線y=ax2+bx+c的頂點坐標是（0.5，-5）

  C．拋物線的對稱軸是直線 x = - 1 2

  D．y的最小值是-5
  組卷：47引用：1難度：0.5

  解析

三、解答題（本大題共8個小題.解答時應寫出必要的文字說明、證明過程或演算步驟）

• 22．綜合與探究．
  問題情境：
  某商店購進一種冬季取暖的“小太陽”取暖器，每臺進價為40元．這種取暖器的銷售價為每臺52元時，每周可售出180臺．
  探究發(fā)現(xiàn)：
  ①銷售定價每增加1元時，每周的銷售量將減少10臺；
  ②銷售定價每降低1元時，每周的銷售量將增多10臺．
  問題解決：
  若商店準備把這種取暖器銷售價定為每臺x元，每周銷售獲利為y元．
  （1）當x=54時，這周的“小太陽”取暖器的銷售量為

  臺，每周銷售獲利y為

  元．
  （2）求y與x的函數(shù)關系式（不必寫出x的取值范圍），并求出銷售價定為多少時，這周銷售“小太陽”取暖器獲利最大，最大利潤是多少？
  （3）若該商店在某周銷售這種“小太陽”取暖器獲利2000元，求x的值．
  組卷：113引用：1難度：0.6

  解析

• 23．綜合與實踐．
  如圖，拋物線

  y

  =

  1

  2

  x

  2

  -

  x

  -

  4

  與x軸交于A和B兩點（點B在點A的右側），與y軸交于點C，拋物線的頂點是點D．
  （1）求點A，B，C和點D四點的坐標；
  （2）如圖1，連接DB，DC和BC，求△BDC的面積；
  （3）點E在拋物線的對稱軸上運動，△BCE是以BC為直角邊的直角三角形，借助圖2，直接寫出點E的坐標．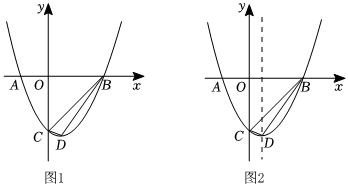
  
  組卷：188引用：1難度：0.3

  解析