2023-2024學年吉林省通化市梅河口五中高三（上）開學數(shù)學試卷

一、選擇題：本題共8小題，每小題5分，共40分.在每小題所給的四個選項中，只有一項是符合題目要求的.

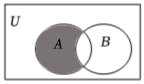• 1．設全集U=R，A={x|0＜x≤3}，B={x|x＜1}，則圖中陰影部分表示的集合為（　　）

  A．{x|1≤x＜3}

  B．{x|1＜x≤3}

  C．{x|1＜x＜3}

  D．{x|1≤x≤3}
  組卷：53引用：5難度：0.7

  解析

• 2．已知

  a

  ∈

  R

  ，

  z

  =

  a

  +

  i

  1

  +

  i

  （i為虛數(shù)單位）是純虛數(shù)，則a=（　　）

  A．-1

  B．0

  C．1

  D．2
  組卷：20引用：1難度：0.8

  解析

• 3．已知雙曲線C：

  x

  2

  4

  -

  y

  2

  b

  2

  =1（b＞0）的一條漸近線方程為y=

  1

  2

  x,則C的焦距為（　　）

  A． 3

  B． 5

  C．2 3

  D．2 5
  組卷：196引用：3難度：0.9

  解析

• 4．《幾何原本》是古希臘數(shù)學家歐幾里得的一部不朽之作，其第十一卷中稱軸截面為等腰直角三角形的圓錐為直角圓錐．如圖，若AB，CD都是直角圓錐SO底面圓的直徑，且

  ∠

  AOD

  =

  π

  3

  ，則異面直線SA與BD所成角的余弦值為（　　）

  A． 1 3

  B． 2 4

  C． 6 4

  D． 6 3
  組卷：343引用：8難度：0.7

  解析

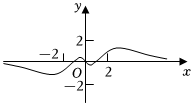• 5．已知函數(shù)f（x）的部分圖象如圖所示，則函數(shù)f（x）的解析式可能為（　　）

  A． f （ x ） = x - x 3 2 x	B．f（x）=e|x|?（x2-1）
  C．f（x）=x3?ln|x|	D． f （ x ） = x 3 - x e | x |
  組卷：230引用：2難度：0.8

  解析

• 6．已知集合A={x∈N|x²＜8x}，B={2，3，6}，C={2，3，7}，則B∪（?_AC）=（　　）

  A．{2，3，4，5}	B．{2，3，4，5，6}
  C．{1，2，3，4，5，6}	D．{1，3，4，5，6，7}
  組卷：59引用：5難度：0.8

  解析

• 7．已知復數(shù)z=

  5

  3

  +

  4

  i

  ，則復數(shù)z的虛部為（　　）

  A． 4 5

  B． - 4 5

  C． 4 5 i

  D． - 4 5 i
  組卷：67引用：2難度：0.8

  解析

四、解答題（本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟）

• 21．已知函數(shù)f（x）=mx²（ln x+

  1

  2

  ）．
  （Ⅰ）若m=1，求曲線y=f（x）在（1，f（1））處的切線方程；
  （Ⅱ）當m≤1時，要使f（x）＞xlnx恒成立，求實數(shù)m的取值范圍．
  組卷：127引用：3難度：0.3

  解析

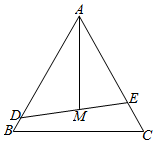• 22．某公園有一塊邊長為3百米的正三角形ABC空地，擬將它分割成面積相等的三個區(qū)域，用來種植三種花卉．方案是：先建造一條直道DE將△ABC分成面積之比為2：1的兩部分（點D，E分別在邊AB，AC上）；再取DE的中點M，建造直道AM（如圖）．設AD=x,DE=y₁，AM=y₂（單位：百米）．
  （1）分別求y₁，y₂關于x的函數(shù)關系式；
  （2）試確定點D的位置，使兩條直道的長度之和最小，并求出最小值．
  組卷：167引用：3難度：0.4

  解析