當前位置：試卷中心 > 試卷詳情

2022-2023學年湖北省荊州市沙市中學高一（下）期中數學試卷

發布：2024/5/11 8:0:9

一、單選題（每題5分，共40分）

1．復數
2
1
+
i
（i為虛數單位）的虛部是（　　）
A．1 B．-1 C．-i D．i
組卷：19引用：9難度：0.9
解析
2．設集合
A
=
{
x
|
y
=
x
-
1
}
，
B
=
{
y
|
y
=
cos
（
π
4
-
x
）
，
x
∈
[
0
，
π
2
]
}
，則A∪B=（　　）
A．[1，+∞） B．
[
2
2
，
1
]
C．
[
2
2
，
+
∞
）
D．R
組卷：16引用：1難度：0.9
解析
3．已知
AB
=
a
+
5
b
，
BC
=
-
2
a
+
8
b
，
CD
=
3
（
a
-
b
）
，則（　　）
A．A、B、D三點共線 B．A、B、C三點共線
C．B、C、D三點共線 D．A、C、D三點共線
組卷：893引用：37難度：0.9
解析
4．在△ABC中，“cosA=2sinBsinC”是“△ABC為鈍角三角形”的（　　）
A．必要不充分條件 B．充要條件
C．充分不必要條件 D．既不充分也不必要條件
組卷：27引用：9難度：0.9
解析
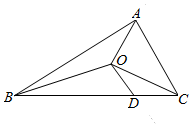5．如圖，O是△ABC的重心，
AB
=
a
，
AC
=
b
，D是邊BC上一點，且
BD
=3
DC
，則（　　）
A．
OD
=
-
1
12
a
+
5
12
b
B．
OD
=
1
12
a
-
5
12
b
C．
OD
=
-
1
12
a
-
5
12
b
D．
OD
=
1
12
a
+
5
12
b
組卷：901引用：7難度：0.7
解析
6．某種藥物作用在農作物上的分解率為v,與時間t（小時）滿足函數關系式v=ab^t（其中a,b為非零常數），若經過12小時該藥物的分解率為10%，經過24小時該藥物的分解率為20%，那么這種藥物完全分解，至少需要經過（　　）（參考數據：lg2≈0.3）
A．48小時 B．52小時 C．64小時 D．120小時
組卷：162引用：5難度：0.8
解析
7．若sin2α=
5
5
，sin（β-α）=
10
10
，且α∈
[
π
4
，
π
]
，β∈[π，
3
π
2
]，則a+β的值是（　　）
A．
5
π
4
B．
7
π
4
C．
5
π
4
或
7
π
4
D．
5
π
4
或
9
π
4
組卷：823引用：4難度：0.8
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四．解答題（共70分）

21．已知向量
m
=
（
sin
2
x
,
cos
2
x
）
，
n
=
（
3
2
，
1
2
）
，函數
f
（
x
）
=
m
?
n
．
（1）求函數f（x）的解析式和對稱軸方程；
（2）若a,b,c分別為△ABC三個內角A，B，C的對邊，f（A）=1，b=2，
a
∈
[
1
2
，
5
2
]
，試判斷這個三角形解的個數，并說明理由；
（3）若
x
∈
[
-
π
6
，
2
π
3
]
時，關于x的方程
f
（
x
+
π
6
）
+
（
λ
+
1
）
sinx
=
λ
（
λ
∈
R
）
恰有三個不同的實根x₁，x₂，x₃，求實數λ的取值范圍及x₁+x₂+x₃的值．
組卷：45引用：1難度：0.4
解析
22．定義非零向量
OM
=（a,b）的“相伴函數”為f（x）=asinx+bcosx（x∈R），向量
OM
=（a,b）稱為函數f（x）=asinx+bcosx（x∈R）的“相伴向量”（其中O為坐標原點）．記平面內所有向量的“相伴函數”構成的集合為S．
（1）設h（x）=
3
cos（x+
π
6
）+3cos（
π
3
-x）（x∈R），請問函數h（x）是否存在相伴向量
OM
，若存在，求出與
OM
共線的單位向量；若不存在，請說明理由．
（2）已知點M（a,b）滿足：
b
a
∈
（
0
，
3
]，向量
OM
的“相伴函數”f（x）在x=x₀處取得最大值，求tan2x₀的取值范圍．
組卷：401引用：8難度：0.1
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．A、B、D三點共線	B．A、B、C三點共線
C．B、C、D三點共線	D．A、C、D三點共線

A．必要不充分條件	B．充要條件
C．充分不必要條件	D．既不充分也不必要條件

A． OD = - 1 12 a + 5 12 b	B． OD = 1 12 a - 5 12 b
C． OD = - 1 12 a - 5 12 b	D． OD = 1 12 a + 5 12 b

2022-2023學年湖北省荊州市沙市中學高一（下）期中數學試卷

一、單選題（每題5分，共40分）

1．復數21+i（i為虛數單位）的虛部是（ ）

2．設集合A={x|y=x-1}，B={y|y=cos（π4-x），x∈[0，π2]}，則A∪B=（ ）

3．已知AB=a+5b，BC=-2a+8b，CD=3（a-b），則（ ）

4．在△ABC中，“cosA=2sinBsinC”是“△ABC為鈍角三角形”的（ ）

5．如圖，O是△ABC的重心，AB=a，AC=b，D是邊BC上一點，且BD=3DC，則（ ）

7．若sin2α=55，sin（β-α）=1010，且α∈[π4，π]，β∈[π，3π2]，則a+β的值是（ ）

四．解答題（共70分）

1．復數
2
1
+
i
（i為虛數單位）的虛部是（　　）

2．設集合
A
=
{
x
|
y
=
x
-
1
}
，
B
=
{
y
|
y
=
cos
（
π
4
-
x
）
，
x
∈
[
0
，
π
2
]
}
，則A∪B=（　　）

3．已知
AB
=
a
+
5
b
，
BC
=
-
2
a
+
8
b
，
CD
=
3
（
a
-
b
）
，則（　　）

4．在△ABC中，“cosA=2sinBsinC”是“△ABC為鈍角三角形”的（　　）

5．如圖，O是△ABC的重心，
AB
=
a
，
AC
=
b
，D是邊BC上一點，且
BD
=3
DC
，則（　　）

7．若sin2α=
5
5
，sin（β-α）=
10
10
，且α∈
[
π
4
，
π
]
，β∈[π，
3
π
2
]，則a+β的值是（　　）