2022-2023學年山東省臨沂市沂水縣高一（下）期中數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．若直線a在平面γ外，則（　　）

  A．a∥γ	B．a與γ至少有一個公共點
  C．a∩γ=A	D．a與γ至多有一個公共點
  組卷：235引用：5難度：0.9

  解析

• 2．sin20°cos10°+sin10°sin70°的值是（　　）

  A． 1 4

  B．- 3 2

  C． 1 2

  D．- 3 4
  組卷：528引用：8難度：0.9

  解析

• 3．已知A（1，0），B（5，-2），C（8，4），D（4，6），則四邊形ABCD為（　　）

  A．正方形

  B．菱形

  C．梯形

  D．矩形
  組卷：55引用：3難度：0.9

  解析

• 4．已知

  2

  sinα

  -

  cosα

  =

  0

  ，則cos2α=（　　）

  A． - 1 3

  B． - 2 3

  C． 1 3

  D． 2 3
  組卷：118引用：1難度：0.8

  解析

• 5．如圖，在正方體ABCD-A₁B₁C₁D₁的八個頂點中，有四個頂點A，B₁，C，D₁恰好是正四面體的頂點，則此正四面體的表面積與正方體的表面積之比為（　　）
  

  A． 3 ： 1

  B． 1 ： 2

  C． 6 ： 2

  D． 3 ： 3
  組卷：160引用：2難度：0.7

  解析

• 6．如圖，為了測量河對岸的塔高AB，測量者選取了與塔底B在同一水平面內的兩個測量基點C與D，并測得

  CD

  =

  20

  2

  m

  ，∠BDC=135°，∠BCD=15°，在點C處測得塔頂A的仰角為60°，則塔高AB=（　　）
  

  A． 30 3 m

  B． 40 3 m

  C． 20 3 m

  D． 40 2 m
  組卷：65引用：1難度：0.6

  解析

• 7．已知AB是⊙O的弦，且

  AB

  =

  3

  ，則

  AB

  ?

  OA

  =（　　）

  A． - 3 2

  B． - 3 4

  C． 3 4

  D． 3 2
  組卷：33引用：1難度：0.7

  解析

四、解答題：本大題共6小題，共70分．解答應寫出文字說明，證明過程或演算步驟．

• 21．已知函數

  f

  （

  x

  ）

  =

  2

  cosx

  （

  2

  sinx

  +

  cosx

  ）

  -

  1

  ．
  （1）求f（x）最小正周期；
  （2）將函數y=f（x）的圖象的橫坐標縮小為原來的

  1

  2

  ，再將得到的函數圖象向右平移

  π

  8

  個單位，最后得到函數y=g（x），求函數g（x）的單調遞增區間；
  （3）若|g（x）-m|≤2在

  [

  0

  ，

  π

  4

  ]

  上恒成立，求實數m的取值范圍．
  組卷：13引用：1難度：0.5

  解析

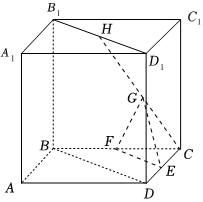• 22．如圖，在正方體ABCD-A₁B₁C₁D₁中，H是B₁D₁的中點，E，F，G分別是DC，BC，HC的中點．求證：
  （1）證明：F，G，H，B四點共面；
  （2）平面EFG∥平面BDD₁B₁；
  （3）若正方體棱長為1，過A，E，C₁三點作正方體的截面，畫出截面與正方體的交線，并求出截面的面積．
  組卷：135引用：1難度：0.5

  解析