2022-2023學年天津市寶坻一中高二（下）第一次段考數學試卷

一、選擇題.（45分）

• 1．下列各式正確的是（　　）

  A．（cosx）′=sinx	B．（ax）′=axlna
  C． （ sin π 12 ） ′ = cos π 12	D． （ x - 5 ） ′ = - 1 5 x - 6
  組卷：382引用：8難度：0.9

  解析

• 2．若

  C

  2

  n

  =15，則

  A

  2

  n

  =（　　）

  A．30

  B．20

  C．12

  D．6
  組卷：334引用：10難度：0.9

  解析

• 3．函數y=f（x）在R上可導，且f（x）=2x²-f'（1）?x-3，則f（1）+f'（1）=（　　）

  A．0

  B．1

  C．-1

  D．不確定
  組卷：1060引用：10難度：0.8

  解析

• 4．函數y=x²e^x的大致圖象為（　　）

  A．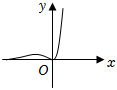

  B．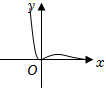

  C．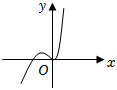

  D．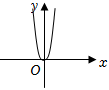
  組卷：198引用：5難度：0.8

  解析

• 5．若5名女生和2名男生去兩地參加志愿者活動，兩地均要求既要有女生又要有男生，則不同的分配方案有（　　）種．

  A．20

  B．40

  C．60

  D．80
  組卷：342引用：6難度：0.6

  解析

• 6．現要從A，B，C，D，E這5人中選出4人，安排在甲、乙、丙、丁4個崗位上，如果A不能安排在甲崗位上，則安排的方法有（　　）

  A．56種

  B．64種

  C．72種

  D．96種
  組卷：946引用：12難度：0.7

  解析

三、解答題

• 19．已知函數f（x）=lnx-ax（a∈R）．
  （1）若x=1是f（x）的極值點，求a的值；
  （2）求函數f（x）的單調區間；
  （3）若函數f（x）在[1，e²]上有且僅有2個零點，求a的取值范圍．
  組卷：586引用：10難度：0.5

  解析

• 20．已知函數f（x）=e^x-1-x-ax²．
  （Ⅰ）當a=0時，
  （ⅰ）求f（x）在點（1，f（1））處的切線方程；
  （ⅱ）求f（x）的最小值；
  （Ⅱ）當x≥0時，若不等式f（x）≥0恒成立，求實數a的取值范圍；
  （Ⅲ）當x＞0時，證明（e^x-1）ln（x+1）＞x²．
  組卷：383引用：4難度：0.3

  解析