2023-2024學年云南省大理州南澗縣民族中學高二（上）見面數學試卷

一、單選題（本題共8小題，每小題5分，共40分，在每小題給出的四個選項中，有且只有一個選項符合題目的要求）

• 1．已知全集U=R，A={x|x≤0}，B={x|x≥1}，則集合?_U（A∪B）=（　　）

  A．{x|x≥0}

  B．{x|x≤1}

  C．{x|0≤x≤1}

  D．{x|0＜x＜1}
  組卷：1801引用：101難度：0.9

  解析

• 2．已知向量

  a

  =（m-1，1），

  b

  =（m,-2），則“m=2”是“

  a

  ⊥

  b

  ”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：825引用：12難度：0.9

  解析

• 3．函數f（x）=log₂x-

  1

  x

  的零點所在的區間為（　　）

  A．（0，1）

  B．（1，2）

  C．（2，3）

  D．（3，4）
  組卷：2239引用：30難度：0.9

  解析

• 4．某同學先后投擲一枚骰子兩次，第一次向上的點數記為x,第二次向上的點數記為y,在直角坐標系xoy中，以（x,y）為坐標的點落在直線2x-y=1上的概率為（　　）

  A． 1 12

  B． 1 9

  C． 5 36

  D． 1 6
  組卷：899引用：11難度：0.9

  解析

• 5．已知m,n是兩條不同的直線，α，β，γ是三個不同的平面，則下列命題中正確的是（　　）

  A．m∥α，n∥α，則m∥n	B．m∥n,m∥α，則n∥α
  C．m⊥α，m⊥β，則α∥β	D．α⊥γ，β⊥γ，則α∥β
  組卷：1271引用：9難度：0.9

  解析

• 6．已知角α的終邊在直線y=2x上，則sinα的值為（　　）

  A．±2

  B． 2 5 5

  C． ± 2 5 5

  D． ± 5 5
  組卷：390引用：3難度：0.7

  解析

• 7．在△ABC中，AD為BC邊上的中線，E為AD的中點，則

  EB

  =（　　）

  A． 3 4 AB - 1 4 AC

  B． 1 4 AB - 3 4 AC

  C． 3 4 AB + 1 4 AC

  D． 1 4 AB + 3 4 AC
  組卷：17694引用：172難度：0.9

  解析

四、解答題（本題滿分70分，解答應寫出文字說明，證明過程和演算步驟.）

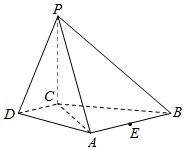• 21．如圖，在四棱錐P-ABCD中，PC⊥平面ABCD，AB∥DC，DC⊥AC．
  （1）求證：DC⊥平面PAC；
  （2）求證：平面PAB⊥平面PAC；
  （3）設點E為AB的中點，在棱PB上是否存在點F，使得PA∥平面CEF？說明理由．
  組卷：7132引用：15難度：0.3

  解析

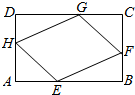• 22．如圖，有一塊矩形空地ABCD，要在這塊空地上開辟一個內接四邊形EFGH為綠地，使其四個頂點分別落在矩形的四條邊上，已知AB=a（a＞2），BC=2，且AE=AH=CF=CG，設AE=x,綠地EFGH面積為y.
  （1）寫出y關于x的函數解析式，并求出它的定義域；
  （2）當AE為何值時，綠地面積y最大？并求出最大值．
  組卷：131引用：7難度：0.3

  解析