2022-2023學年湖北省武漢市部分重點中學(六校聯考)高一(下)期中數學試卷
發布:2024/7/8 8:0:10
一、選擇題:本題共8小題,每小題5分,共40分:在每小題給出的四個選項中,只有一項是符合題目要求的.
-
1.已知復數z滿足z(1+i)=|1-i|,i為虛數單位,則z=( )
A.i B. 22-22iC. 12+12iD. 22+22i組卷:168引用:8難度:0.8 -
2.已知向量
,a=(1,2),b=(1,-1).若c=(4,5)與a垂直,則實數λ的值為( )b+λcA. 114B. -47C.3 D. 411組卷:214引用:6難度:0.7 -
3.下列說法正確的是( )
A.各側面都是正方形的四棱柱一定是正方體 B.球的直徑是連接球面上兩點并且經過球心的線段 C.以直角三角形的一邊所在直線為軸旋轉一周所得的旋轉體是圓錐 D.用一個平面截圓錐,得到一個圓錐和圓臺 組卷:248引用:10難度:0.7 -
 4.如圖所示,點E為△ABC的邊AC的中點,F為線段BE上靠近點B的三等分點,則=( )AF
4.如圖所示,點E為△ABC的邊AC的中點,F為線段BE上靠近點B的三等分點,則=( )AFA. 13BA+23BCB. 43BA+23BCC. -56BA+16BCD. -23BA+13BC組卷:253引用:9難度:0.7 -
 5.如圖,四邊形ABCD的斜二測畫法的直觀圖為等腰梯形A'B'C'D',已知A'B'=4,C'D'=2,則下列說法正確的是( )
5.如圖,四邊形ABCD的斜二測畫法的直觀圖為等腰梯形A'B'C'D',已知A'B'=4,C'D'=2,則下列說法正確的是( )A.AB=2 B. A′D′=22C.四邊形ABCD的周長為 4+22+23D.四邊形ABCD的面積為 62組卷:548引用:31難度:0.6 -
6.已知角α滿足
,則sin2α+3cos2α的值為( )2sin(α-π3)=(2-3)cosαA. 25B. 45C. 75D. 85組卷:134引用:3難度:0.8 -
 7.如圖,一個矩形邊長為1和4,繞它的長為4的邊旋轉二周后所得如圖的一開口容器(下表面密封),P是BC中點,現有一只螞蟻位于外壁A處,內壁P處有一米粒,若這只螞蟻要先爬到上口邊沿再爬到點P處取得米粒,則它所需經過的最短路程為( )
7.如圖,一個矩形邊長為1和4,繞它的長為4的邊旋轉二周后所得如圖的一開口容器(下表面密封),P是BC中點,現有一只螞蟻位于外壁A處,內壁P處有一米粒,若這只螞蟻要先爬到上口邊沿再爬到點P處取得米粒,則它所需經過的最短路程為( )A. π2+36B. π2+16C. 4π2+36D. 4π2+1組卷:88引用:3難度:0.7
四、解答題:本題共6小題,共70分.解答題應寫出文字說明、證明過程或演算步驟.
-
21.已知△ABC的內角,A,B,C的對邊為a,b,c,且
.3(a-b)c=3sinC-2sinBsinA+sinB
(1)求cosA;
(2)若△ABC的面積為為內角A的角平分線,交BC邊于點D,求線段AD長的最大值.22,AD組卷:238引用:3難度:0.5 -
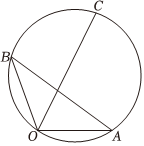 22.如圖,已知與|OA|=1,|OB|=2,OA的夾角為OB,點C是△ABO的外接圓優弧2π3上的一個動點(含端點A,B),記?AB與OA的夾角為θ.OC
22.如圖,已知與|OA|=1,|OB|=2,OA的夾角為OB,點C是△ABO的外接圓優弧2π3上的一個動點(含端點A,B),記?AB與OA的夾角為θ.OC
(1)求△ABO外接圓的直徑2R;
(2)試將表示為θ的函數;|OC|
(3)設點M滿足,若AM=13AB,其中x,y∈R,求OC=xOA+yOB的最大值.OC?OM組卷:109引用:4難度:0.5


