2022-2023學年江蘇省鹽城市、南京市高三（上）期末數學試卷

一、單項選擇題（本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．“a₃+a₉=2a₆”是“數列{a_n}為等差數列”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分又不必要條件
  組卷：99引用：4難度：0.7

  解析

• 2．若復數z滿足|z-1|≤2，則復數z在復平面內對應點組成圖形的面積為（　　）

  A．π

  B．2π

  C．3π

  D．4π
  組卷：130引用：4難度：0.8

  解析

• 3．已知集合

  A

  =

  {

  x

  |

  x

  -

  1

  x

  -

  a

  ＜

  0

  }

  ．若A∩N^*=?，則實數a的取值范圍是（　　）

  A．{1}

  B．（-∞，1）

  C．[1，2]

  D．（-∞，2]
  組卷：56引用：2難度：0.9

  解析

• 4．把5個相同的小球分給3個小朋友，使每個小朋友都能分到小球的分法有（　　）

  A．4種

  B．6種

  C．21種

  D．35種
  組卷：258引用：5難度：0.8

  解析

• 5．某研究性學習小組發現，由雙曲線

  C

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的兩漸近線所成的角可求離心率e的大小，聯想到反比例函數

  y

  =

  k

  x

  （

  k

  ≠

  0

  ）

  的圖象也是雙曲線，據此可進一步推斷雙曲線

  y

  =

  5

  x

  的離心率為（　　）

  A． 2

  B．2

  C． 5

  D．5
  組卷：88引用：2難度：0.8

  解析

• 6．△ABC中，AH為BC邊上的高且

  BH

  =

  3

  HC

  ，動點P滿足

  AP

  ?

  BC

  =

  -

  1

  4

  BC

  2

  ，則點P的軌跡一定過△ABC的（　　）

  A．外心

  B．內心

  C．垂心

  D．重心
  組卷：268引用：4難度：0.5

  解析

• 7．若函數f（x）=x³+bx²+cx+d滿足f（1-x）+f（1+x）=0對一切實數x恒成立，則不等式f'（2x+3）＜f'（x-1）的解集為（　　）

  A．（0，+∞）	B．（-∞，-4）
  C．（-4，0）	D．（-∞，-4）∪（0，+∞）
  組卷：261引用：5難度：0.6

  解析

四、解答題（本大題共6小題，共70分.解答時應寫出必要的文字說明，證明過程或演算步驟）

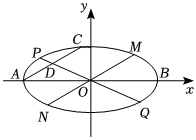• 21．如圖，已知橢圓

  x

  2

  4

  +

  y

  2

  =

  1

  的左、右頂點分別為A，B，點C是橢圓上異于A，B的動點，過原點O平行于AC的直線與橢圓交于點M，N，AC的中點為點D，直線OD與橢圓交于點P，Q，點P，C，M在x軸的上方．
  （1）當

  |

  AC

  |

  =

  5

  時，求cos∠POM；
  （2）求|PQ|?|MN|的最大值．
  組卷：136引用：3難度：0.5

  解析

• 22．已知函數

  f

  （

  x

  ）

  =

  x

  +

  1

  e

  x

  ．
  （1）當x＞-1時，求函數g（x）=f（x）+x²-1的最小值；
  （2）已知x₁≠x₂，f（x₁）=f（x₂）=t,求證：

  |

  x

  1

  -

  x

  2

  |

  ＞

  2

  1

  -

  t

  ．
  組卷：129引用：3難度：0.4

  解析