2022-2023學年山西省太原市小店區山西大學附中高二（上）期中數學試卷

一、單選題（每小題5分，共60分）

• 1．已知點A（1，0），B（2，

  3

  ），則直線AB的傾斜角是（　　）

  A．60°

  B．120°

  C．30°

  D．150°
  組卷：585引用：5難度：0.7

  解析

• 2．已知圓（x-1）²+y²=4內一點P（2，1），則過P點的最短弦所在的直線方程是（　　）

  A．x-y-1=0

  B．x+y-3=0

  C．x+y+3=0

  D．x=2
  組卷：393引用：8難度：0.7

  解析

• 3．直線3x+4y+5=0關于直線x=1對稱的直線方程為（　　）

  A．3x-4y+13=0

  B．3x-4y-11=0

  C．3x+4y-11=0

  D．3x+4y+13=0
  組卷：153引用：2難度：0.7

  解析

• 4．“a=-1”是“直線l₁：（a+2）x+（1-a）y-1=0與l₂：（a-1）x+（2a+3）y+2=0互相垂直”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．即不充分也不必要條件
  組卷：200引用：5難度：0.7

  解析

• 5．若兩條平行直線l₁：x-2y+m=0（m＞0）與l₂：x+ny-3=0之間的距離是

  5

  ，則m+n=（　　）

  A．0

  B．1

  C．-2

  D．-1
  組卷：140引用：4難度：0.7

  解析

• 6．以下四個命題表述正確的是（　　）

  A．直線mx+4y-12=0（m∈R）恒過定點（3，0）

  B．兩圓x2+y2+4x-4y=0與x2+y2+2x-12=0的公共弦所在的直線方程為x+2y+6=0

  C．已知圓C：x2+y2=2，P為直線 x + y + 2 3 = 0 上一動點，過點P向圓C引條切線PA，其中A為切點，則PA的最小值為 2

  D．圓C1：x2+y2+2x=0與圓C2：x2+y2-4x-8y+4=0恰有三條公切線
  組卷：19引用：2難度：0.5

  解析

• 7．已知中心在原點，焦點在x軸上，焦距為4的橢圓被直線l：y=x+3截得的弦的中點的橫坐標為-2，則此橢圓的方程為（　　）

  A． x 2 4 + y 2 2 = 1

  B． x 2 6 + y 2 2 = 1

  C． x 2 8 + y 2 4 = 1

  D． x 2 12 + y 2 8 = 1
  組卷：221引用：5難度：0.5

  解析

三、解答題（17題10分，其余每題12分）

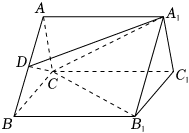• 21．如圖，在三棱柱ABC-A₁B₁C₁中，△ABC為等邊三角形，四邊形BCC₁B₁是邊長為2的正方形，D為AB中點，且

  A

  1

  D

  =

  5

  ．
  （1）求證：CD⊥平面ABB₁A₁；
  （2）若點P在線段B₁C上，且直線AP與平面A₁CD所成角的正弦值為

  2

  5

  5

  ，求點P到平面A₁CD的距離．
  組卷：736引用：12難度：0.6

  解析

• 22．已知點P（1，1）在橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （a＞b＞0）上，橢圓C的左、右焦點分別為F₁，F₂，△PF₁F₂的面積為

  6

  2

  ．
  （1）求橢圓C的方程；
  （2）設點A，B在橢圓C上，直線PA，PB均與圓O：x²+y²=r²（0＜r＜1）相切，試判斷直線AB是否過定點，并證明你的結論．
  組卷：125引用：5難度：0.6

  解析