2023年湘豫名校聯考高考數學一模試卷（文科）

一、選擇題：本題共12小題，每小題5分，共60分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．已知集合A={x∈R|x²-2x-3≤0}，B={x∈R||x-2|＜1}，則A∩B=（　　）

  A．（1，3]

  B．[1，3]

  C．[1，3）

  D．（1，3）
  組卷：15引用：2難度：0.8

  解析

• 2．已知復數z滿足

  5

  1

  -

  2

  i

  =

  z

  ，則|z-i|=（　　）

  A． 5

  B． 2

  C． 6

  D． 2 2
  組卷：13引用：2難度：0.8

  解析

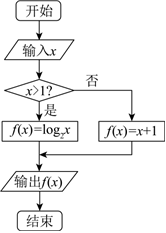• 3．如圖所示的程序框圖中，若輸出的函數值

  f

  （

  x

  ）

  =

  1

  2

  ，則輸入的實數x=（　　）

  A． - 1 2

  B． 2

  C． 2 2

  D． - 1 2 或 2
  組卷：4引用：2難度：0.7

  解析

• 4．已知定義在R上的函數f（x）滿足f（2+x）+f（2-x）=0，函數f（x-1）的圖象關于直線x=1對稱，且f（1）=1，則f（2023）=（　　）

  A．-1

  B．0

  C．1

  D．2
  組卷：177引用：5難度：0.6

  解析

• 5．為慶祝黨的二十大的勝利召開，某高校黨委從所有的學生黨員中隨機抽取100名，舉行“二十大”相關知識的競賽活動，根據競賽成績，得到如表2×2列聯表．則下列說法正確的是（　　）
  

  	優秀	非優秀	合計
  男	20	30	50
  女	35	15	50
  合計	55	45	100

  參考公式及數據：

  K

  2

  =

  n

  （

  ad

  -

  bc

  ）

  2

  （

  a

  +

  b

  ）

  （

  c

  +

  d

  ）

  （

  a

  +

  c

  ）

  （

  b

  +

  d

  ）

  ，其中n=a+b+c+d.
  

  P（K2≥k0）	0.10	0.05	0.025	0.010	0.005	0.001
  k0	2.706	3.841	5.024	6.635	7.879	10.828

  A．有99.5%的把握認為“競賽成績是否優秀與性別有關”

  B．有99.5%的把握認為“競賽成績是否優秀與性別無關”

  C．在犯錯誤的概率不超過0.001的前提下，認為“競賽成績是否優秀與性別無關”

  D．在犯錯誤的概率不超過0.001的前提下，認為“競賽成績是否優秀與性別有關”
  組卷：136引用：3難度：0.7

  解析

• 6．已知實數x,y滿足約束條件

  x ≤ 3 ，

  x + y ≥ 0 ，

  x - y + 2 ≥ 0 ，

  則|x-2y|的最大值是（　　）

  A．5

  B．6

  C．7

  D．9
  組卷：15引用：3難度：0.6

  解析

• 7．已知函數

  f

  （

  x

  ）

  =

  sin

  （

  ωx

  +

  π

  6

  ）

  （

  ω

  ＞

  0

  ）

  在區間

  （

  0

  ，

  π

  2

  ）

  上的極值點有且僅有2個，則ω的取值范圍是（　　）

  A． （ 8 3 ， 11 3 ]

  B． [ 8 3 ， 11 3 ）

  C． （ 8 3 ， 14 3 ]

  D． [ 8 3 ， 14 3 ）
  組卷：57引用：3難度：0.7

  解析

（二）選考題：共10分、請考生在22、23題中任選一題作答，如果多做，則按所做的第一題計分。[選修4-4：坐標系與參數方程]（10分）

• 22．在平面直角坐標系xOy中，曲線C的參數方程為

  x = - 2 + cosθ ，

  y = - 2 + sinθ

  （θ為參數）．以坐標原點O為極點，x軸正半軸為極軸建立極坐標系，直線l的極坐標方程為ρ（cosθ+sinθ）=-1．
  （1）求曲線C的極坐標方程和直線l的直角坐標方程；
  （2）若直線l與y軸交于點A，點P在曲線C上運動，求直線AP斜率的最大值．
  組卷：14引用：1難度：0.6

  解析

[選修4-5：不等式選講]（10分）

• 23．若函數f（x）=|x-t|+2|x+3|（t＞0）的最小值為5．
  （1）求t的值；
  （2）已知a＞0，b＞0，且a+2b=t,求

  2

  a

  +

  1

  b

  的最小值．
  組卷：9引用：1難度：0.6

  解析