2022-2023學年江西省宜春市上高二中高三（上）第三次月考數學試卷（文科）

一、選擇題：本題共12小題，每小題5分，共60分.

• 1．化簡式子

  （

  1

  8

  ）

  1

  3

  -

  lo

  g

  3

  2

  ×

  lo

  g

  4

  27

  +

  202

  3

  0

  等于（　　）

  A．0

  B． 3 2

  C．-1

  D． 1 2
  組卷：632引用：4難度：0.7

  解析

• 2．若函數g（x）=lnx+

  1

  2

  x

  2

  -（b-1）x存在單調遞減區間，則實數b的取值范圍是（　　）

  A．[3，+∞）

  B．（3，+∞）

  C．（-∞，3）

  D．（-∞，3]
  組卷：126引用：9難度：0.8

  解析

• 3．若{2，3}?M?{1，2，3，4，5}，則M的個數為（　　）

  A．5

  B．6

  C．7

  D．8
  組卷：88引用：3難度：0.7

  解析

• 4．若命題“?x∈（-1，3），x²-2x-a＞0”為假命題，則實數a可取的最小整數值是（　　）

  A．-1

  B．0

  C．2

  D．3
  組卷：5引用：2難度：0.7

  解析

• 5．已知函數y=f（x）=|a^x-a|（a＞0且a≠1）的圖象可能為（　　）

  A．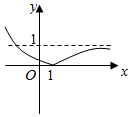

  B．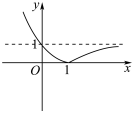

  C．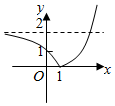

  D．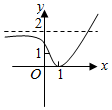
  組卷：180引用：4難度：0.7

  解析

• 6．若α∈（0，π），

  tan

  2

  α

  =

  sinα

  cosα

  +

  2

  ，則

  sin

  （

  α

  +

  5

  π

  6

  ）

  =（　　）

  A． 3 + 15 8

  B． 3 - 15 8

  C． 1 - 3 5 8

  D． - 1 - 3 5 8
  組卷：132引用：3難度：0.7

  解析

• 7．已知函數f（x）的導函數為f'（x），f'（-2）=-2，則

  △

  x

  →

  0

  lim

  f

  （

  -

  2

  -

  4

  △

  x

  ）

  -

  f

  （

  -

  2

  ）

  △

  x

  =（　　）

  A．-8

  B．-2

  C．2

  D．8
  組卷：273引用：3難度：0.8

  解析

三、解答題：共70分.解答應寫出文字說明、證明過程或演算步驟.

• 21．已知函數f（x）=|x-1|+|x-3|．
  （1）解不等式f（x）＜4；
  （2）設M是函數f（x）的最小值，若a,b+2，c+1均為正數，且a+2b+3c=M，求證：

  a

  （

  b

  +

  2

  ）

  （

  c

  +

  1

  ）

  ≤

  9

  M

  ．
  組卷：79引用：5難度：0.5

  解析

• 22．已知函數

  f

  （

  x

  ）

  =

  2

  lnx

  -

  1

  2

  a

  x

  2

  +

  （

  2

  a

  -

  1

  ）

  x

  （

  a

  ＞

  0

  ）

  ．
  （1）若曲線y=f（x）在點（1，f（1））處的切線經過原點，求a的值；
  （2）設g（x）=x²-2x,若對任意s∈（0，2]，均存在t∈（0，2]，使得f（s）＜g（t），求a的取值范圍．
  組卷：106引用：4難度：0.3

  解析