2021-2022學年湖北省武漢市華中師大一附中高一（上）期末數學試卷

一、選擇題：本題共8小題，每小題5分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．設集合M=

  {

  x

  |

  x

  ＞

  （

  1

  10

  ）

  lg

  2

  }

  ，N={x|2^x＞8}，則M∩（?_RN）=（　　）

  A． （ 1 2 ， 3 ）

  B．（2，3）

  C． （ 1 2 ， 3 ]

  D．（2，3]
  組卷：99引用：1難度：0.7

  解析

• 2．下列函數既是奇函數，又在區間[-1，1]上單調遞減的是（　　）

  A．f（x）=sinx

  B．f（x）=-|x+1|

  C．f（x）= 1 2 （ a x + a - x ） （a＞0且a≠1）

  D．f（x）=ln 2 - x 2 + x
  組卷：343引用：20難度：0.7

  解析

• 3．已知冪函數y=x^a的圖象過點

  （

  3

  ，

  1

  9

  ）

  ，則下列兩函數的大小關系為：（x²-2x+4）^a（　　）（-3）^a

  A．≤

  B．≥

  C．＜

  D．＞
  組卷：207引用：1難度：0.7

  解析

• 4．下列四個函數：
  ①y=-x+1，
  ②y=

  x 1 3 ， x ≤ 0

  1 x 3 ， x ＞ 0

  ，
  ③y=ln|x|，
  ④

  y

  =

  2

  x

  -

  1

  x

  -

  2

  ，
  其中定義域和值域相同的函數有（　　）

  A．4個

  B．3個

  C．2個

  D．1個
  組卷：292引用：3難度：0.7

  解析

• 5．下列關于命題“若x＞1，則2x+1＞5”（假命題）的否定，正確的是（　　）

  A．若x＞1，則2x+1≤5

  B．存在一個實數x,滿足x＞1，但2x+1≤5

  C．任意實數x,滿足x＞1，但2x+1≤5

  D．若存在一個實數x,滿足x≤1，則2x+1≤5
  組卷：78引用：2難度：0.9

  解析

• 6．函數

  f

  （

  x

  ）

  =

  4

  x

  -

  4

  -

  x

  x

  2

  +

  |

  x

  |

  -

  2

  的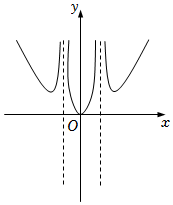圖象大致為（　　）

  A．	B．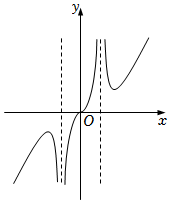
  C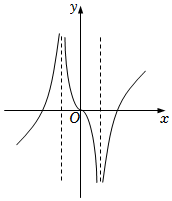．	D．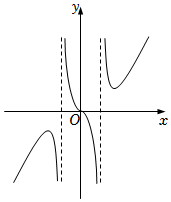
  組卷：181引用：3難度：0.7

  解析

• 7．“函數y=-x³+ax在（0，1）上是增函數”是：“實數a＞3”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：59引用：2難度：0.7

  解析

四、解答題：本題共6小題，共70分，解答應寫出文字說明、證明過程或演算步驟.

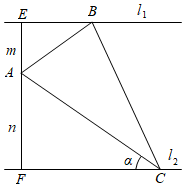• 21．如圖，直線l₁∥l₂，點A是l₁，l₂之間的一個定點，過點A的直線EF⊥l₁，與直線l₁，l₂分別交于點E，F，且AE=m,AF=n（m,n為常數），點B，C分別為直線l₁，l₂上的動點，已知

  ∠

  BAC

  =

  π

  3

  ，設

  ∠

  ACF

  =

  α

  （

  0

  ＜

  α

  ＜

  π

  3

  ）

  ．
  （1）求△ABC的面積關于α的函數解析式f（α）；
  （2）求函數f（α）的最小值．
  組卷：86引用：1難度：0.4

  解析

• 22．已知f（x），g（x）分別是定義在R上的奇函數和偶函數，且f（x）+g（x）=e^x．
  （1）分別求出函數f（x），g（x）的解析式；
  （2）若?x∈（ln（

  2

  -

  1

  ），ln

  5

  -

  1

  2

  ），都有（m²-2）f（x）+mg（2x）-4m＞0成立，求實數m的取值范圍．
  組卷：221引用：1難度：0.3

  解析