2022-2023學年廣東省肇慶市百花中學高二（上）期中數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．已知直線l經過

  A

  （

  1

  ，

  0

  ）

  ，

  B

  （

  4

  ，-

  3

  3

  ）

  兩點，則直線l的傾斜角是（　　）

  A．30°

  B．60°

  C．120°

  D．150°
  組卷：88引用：8難度：0.7

  解析

• 2．已知

  v

  為直線l的方向向量，

  n

  1

  ，

  n

  2

  分別為平面α，β的法向量（α，β不重合），那么下列說法中，正確的有（　　）

  A． n 1 ∥ n 2 ?α∥β

  B． n 1 ⊥ n 2 ?α⊥β

  C． v ∥ n 1 ?l∥α

  D． v ⊥ n 1 ?l⊥α
  組卷：280引用：24難度：0.6

  解析

• 3．若bc＜0，ab＞0，則直線ax+by+c=0的圖象只能是（　　）

  A．

  B．

  C．

  D．
  組卷：66引用：4難度：0.7

  解析

• 4．若異面直線l₁，l₂的方向向量分別是

  a

  =

  （

  0

  ，-

  2

  ，-

  1

  ）

  ，

  b

  =

  （

  2

  ，

  4

  ，

  0

  ）

  ，則異面直線l₁與l₂的夾角的余弦值等于（　　）

  A． - 2 5

  B． 2 5

  C． - 4 5

  D． 4 5
  組卷：313引用：5難度：0.7

  解析

• 5．已知過點P（3，1）的直線與圓（x-1）²+（y-2）²=5相切，且與直線x-my-1=0垂直，則m=（　　）

  A． - 1 2

  B． 1 2

  C．-2

  D．2
  組卷：179引用：3難度：0.8

  解析

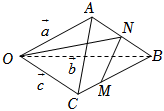• 6．如圖，在三棱錐O-ABC中，設

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，若

  AN

  =

  NB

  ，

  BM

  =

  2

  MC

  ，則

  MN

  =（　　）

  A． 1 2 a + 1 6 b - 2 3 c	B． 1 2 a - 1 6 b + 2 3 c
  C． 1 2 a - 1 6 b - 1 3 c	D． - 1 2 a + 1 6 b + 1 3 c
  組卷：161引用：5難度：0.7

  解析

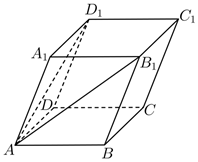• 7．如圖，在平行六面體ABCD-A₁B₁C₁D₁中，AA₁=AD=AB=2，∠BAD=

  π

  2

  ，∠BAA₁=∠A₁AD=

  π

  3

  ，則

  A

  B

  1

  ?

  A

  D

  1

  =（　　）

  A．12

  B．8

  C．6

  D．4
  組卷：100引用：10難度：0.7

  解析

四、解答題：本大題共6小題，共70分，解答應寫出文字說明、證明過程或演算步驟

• 21．如圖，已知PA⊥平面ABCD，底面ABCD為矩形，PA=AD=AB=2，M，N分別為AB，PC的中點．
  （1）求證：MN∥平面PAD；
  （2）求PD與平面PMC所成角的正弦值；
  （3）求平面PMC與平面PAD的夾角的余弦值．
  組卷：6引用：2難度：0.5

  解析

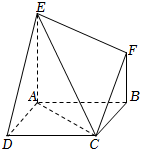• 22．如圖多面體ABCDEF中，四邊形ABCD是菱形，∠ABC=60°，EA⊥平面ABCD，EA∥BF，AB=AE=2BF=2．
  （1）證明：平面EAC⊥平面EFC；
  （2）在棱EC上有一點M，使得平面MBD與平面ABCD的夾角為45°，求點M到平面BCF的距離．
  組卷：456引用：10難度：0.4

  解析