2022-2023學年北京五十七中高二（下）期中數學試卷

一、選擇題共10小題，每小題4分，共40分.在每小題列出的四個選項中，選出符合題目要求的一項。

• 1．已知集合A={x|-1＜x＜1}，B={x|0≤x≤3}，則A∪B=（　　）

  A．[0，1）

  B．[0，1]

  C．（-1，3]

  D．（-1，3）
  組卷：115引用：4難度：0.8

  解析

• 2．在復平面內，復數z對應的點的坐標為（1，-1），則i?z=（　　）

  A．1+i

  B．-1-i

  C．1-i

  D．-1+i
  組卷：115引用：3難度：0.8

  解析

• 3．在等差數列{a_n}中，a₂=1，a₅=5，則a₈=（　　）

  A．9

  B．11

  C．13

  D．15
  組卷：100引用：1難度：0.9

  解析

• 4．已知雙曲線

  x

  2

  4

  -

  y

  2

  b

  2

  =

  1

  （

  b

  ＞

  0

  ）

  的離心率是2，則b=（　　）

  A．12

  B． 2 3

  C． 3

  D． 3 2
  組卷：470引用：4難度：0.9

  解析

• 5．若點M（1，1）為圓C：x²+y²-4x=0的弦AB的中點，則直線AB的方程是（　　）

  A．x-y-2=0

  B．x+y-2=0

  C．x-y=0

  D．x+y=0
  組卷：428引用：3難度：0.8

  解析

• 6．已知平面向量

  a

  ，

  b

  滿足

  |

  a

  |

  =

  2

  ，|

  b

  |=1，且

  a

  與

  b

  的夾角為

  2

  3

  π

  ，則

  |

  a

  +

  b

  |

  =（　　）

  A． 3

  B． 5

  C． 7

  D．3
  組卷：107引用：1難度：0.8

  解析

• 7．函數y=2^|x|sin2x的圖象可能是（　　）

  A．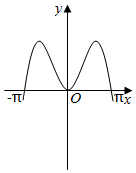

  B．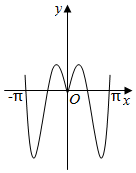

  C．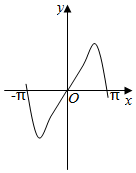

  D．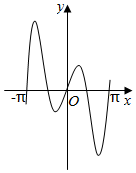
  組卷：8055引用：113難度：0.7

  解析

三、解答題共6小題，共85分.解答應寫出文字說明、演算步驟或證明過程.

• 20．已知數列A：a₁，a₂，…，a_n（0≤a₁＜a₂＜…＜a_n，n≥3），具有性質P：對任意i,j（1≤i≤j≤n）a_j+a_i與a_j-a_i，兩數中至少有一個是該數列中的一項，S_n為數列A的前n項和．
  （Ⅰ）分別判斷數列0，1，3，5與數列0，2，4，6是否具有性質P；
  （Ⅱ）證明：a₁=0，且S_n=

  n

  a

  n

  2

  ；
  （Ⅲ）證明：當n=5時，a₁，a₂，a₃，a₄，a₅成等差數列．
  組卷：231引用：2難度：0.2

  解析

• 21．已知集合M={1，2，3，…，n}（n∈N^*），若集合

  A

  =

  {

  a

  1

  ，

  a

  2

  ，

  a

  3

  ，…，

  a

  m

  }

  （

  m

  ∈

  N

  *

  ）

  ，且對任意的b∈M，存在a_i，a_j∈A（1≤i≤j≤m），使得b=λ₁a_i+λ₂a_j（其中λ₁，λ₂∈{-1，0，1}），則稱集合A為集合M的一個m元基底．
  （Ⅰ）分別判斷下列集合A是否為集合M的一個二元基底，并說明理由；
  ①A={1，5}M={1，2，3，4，5}；
  ②A={2，3}，M={1，2，3，4，5，6}．
  （Ⅱ）若集合A是集合M的一個m元基底，證明：m（m+1）≥n；
  （Ⅲ）若集合A為集合M={1，2，3，…，19}的一個m元基底，求出m的最小可能值，并寫出當m取最小值時M的一個基底A．
  組卷：134引用：6難度：0.1

  解析