2022-2023學年安徽省六安市金安區輕工中學八年級（下）期中數學試卷

一、選擇題（本大題共10題，每小題4分，滿分40分）

• 1．下列式子中，屬于最簡二次根式的是（　　）

  A． 9

  B． 7

  C． 20

  D． 1 3
  組卷：4233引用：254難度：0.9

  解析

• 2．下列根式中，與

  12

  為同類二次根式的是（　　）

  A． 3

  B． 2

  C． 6

  D． 32
  組卷：440引用：4難度：0.7

  解析

• 3．估計

  3

  ×（2

  3

  +

  5

  ）的值應在（　　）

  A．10和11之間

  B．9和10之間

  C．8和9之間

  D．7和8之間
  組卷：1110引用：20難度：0.7

  解析

• 4．下列四組線段中，可以構成直角三角形的是（　　）

  A．1、2、3

  B．2、3、4

  C．1、 2 、 3

  D． 2 、3、5
  組卷：32引用：4難度：0.6

  解析

• 5．三角形的三邊長分別為6，8，10，則它的最長邊上的高為（　　）

  A．4.8

  B．8

  C．6

  D．2.4
  組卷：80引用：2難度：0.6

  解析

• 6．若關于x的一元二次方程的兩個根為x₁=1，x₂=2，則這個方程可能是（　　）

  A．x2+3x-2=0

  B．x2+3x+2=0

  C．x2-3x+2=0

  D．x2-2x+3=0
  組卷：1075引用：24難度：0.9

  解析

• 7．若關于x的方程x²+2x-k=0沒有實數根，則k的值可以是（　　）

  A．-2

  B．-1

  C．0

  D．1
  組卷：313引用：8難度：0.6

  解析

七、（本題滿分12分）

• 22．某旅行社為吸引廣大市民組團去H市旅游，推出了如下收費標準：如果人數不超過10人，人均旅游費用為200元，如果人數超過10人，每增加1人，人均旅游費用降低5元，但人均旅游費用不得低于150元．
  （1）如果某單位組織12人參加去H市旅游，那么需支付旅行社旅游費用共

  元；
  （2）現某單位組織員工去H市旅游，共支付給該旅行社旅游費用2625元，那么該單位有多少名員工參加旅游？
  組卷：228引用：3難度：0.5

  解析

八、（本題滿分14分）

• 23．問題發現：如圖1，在Rt△ABC中，AB=AC，D為BC邊所在直線上的一動點（不與點B、C重合），連接AD，以AD為邊作Rt△ADE，且AD=AE，根據∠BAC+∠CAD=∠CAD+∠DAE，得到∠BAD=∠CAE，結合AB=AC，AD=AE得出△BAD≌△CAE，發現線段BD與CE的數量關系為BD=CE，位置關系為BD⊥CE；
  
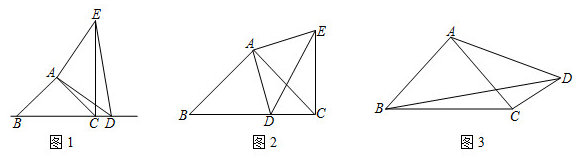
  （1）探究證明：如圖2，在Rt△ABC和Rt△ADE中，AB=AC，AD=AE，且點D在BC邊上滑動（點D不與點B，C重合），連接EC．
  ①則線段BC，DC，EC之間滿足的等量關系式為

  ；
  ②求證：BD²+CD²=2AD²；
  （2）拓展延伸：如圖3，在四邊形ABCD中，∠ABC=∠ACB=∠ADC=45°．若BD=13cm,CD=5cm,求AD的長．
  組卷：532引用：3難度：0.2

  解析