當(dāng)前位置：試卷中心 > 試卷詳情

2023-2024學(xué)年黑龍江省大慶市薩爾圖區(qū)東風(fēng)中學(xué)高二（上）開學(xué)數(shù)學(xué)試卷

發(fā)布：2024/8/19 15:0:1

4．下列說法正確的是（　　）

A．棱柱的兩個互相平行的面一定是棱柱的底面

B．有兩個面平行且相似，其余各面都是梯形的多面體是棱臺

C．如果一個棱錐的各個側(cè)面都是等邊三角形，那么這個棱錐可能為六棱錐

D．如果一個棱柱的所有面都是長方形，那么這個棱柱是長方體

組卷：186引用：4難度：0.8

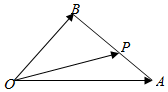5．如圖，在△OAB中，P為線段AB上的一點(diǎn)，
OP
=
x
OA
+
y
OB
，且
BP
=
2
PA
，則（　　）
A．
x
=
2
3
，
y
=
1
3
B．
x
=
1
3
，
y
=
2
3
C．
x
=
1
4
，
y
=
3
4
D．
x
=
3
4
，
y
=
1
4
組卷：305引用：29難度：0.7
解析
6．已知圓錐的側(cè)面展開圖為一個面積為2π的半圓，則該圓錐的高為（　　）
A．
5
2
B．1 C．
2
D．
3
組卷：728引用：7難度：0.8
解析
7．若m,n是兩條不同的直線，α，β，γ是三個不同的平面，則下列為真命題的是（　　）
A．若m?β，α⊥β，則m⊥α B．若m∥α，n∥α，則m∥n
C．若m⊥β，m∥α，則α⊥β D．若α⊥γ，α⊥β，則β⊥γ
組卷：256引用：9難度：0.4
解析

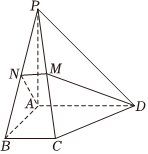21．如圖，在四棱錐P-ABCD中，底面為直角梯形，AD∥BC，∠BAD=90°，PA⊥底面ABCD，且PA=AD=AB=2BC，M、N分別為PC、PB的中點(diǎn)．
（Ⅰ）求證：PB⊥DM；
（Ⅱ）求BD與平面ADMN所成的角．
組卷：735引用：14難度：0.1
解析
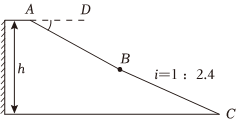22．2022年北京冬奧會的成功舉辦激發(fā)了人們對冰雪運(yùn)動的熱情．如圖是某滑雪場的橫截面示意圖，雪道分為AB，BC兩部分，小明同學(xué)在C點(diǎn)測得雪道BC的坡度i=1：2.4，在A點(diǎn)測得B點(diǎn)的俯角∠DAB=30°．若雪道AB長為270m,雪道BC長為260m.
（1）求該滑雪場的高度h；
（2）據(jù)了解，該滑雪場要用兩種不同的造雪設(shè)備來滿足對于雪量和雪質(zhì)的不同要求，其中甲設(shè)備每小時造雪量比乙設(shè)備少35m³，且甲設(shè)備造雪150m³所用的時間與乙設(shè)備造雪500m³所用的時間相等．求甲、乙兩種設(shè)備每小時的造雪量．
組卷：15引用：2難度：0.5
解析