2023-2024學年河南省濮陽第一高級中學高二（上）月考數學試卷（9月份）

一、選擇題。本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知向量

  a

  =（1，2，1），

  b

  =（-1，0，4），則

  a

  +2

  b

  =（　　）

  A．（-1，2，9）

  B．（-1，4，5）

  C．（1，2，-7）

  D．（1，4，9）
  組卷：438引用：7難度：0.9

  解析

• 2．已知向量

  a

  =

  （

  2

  ，-

  3

  ，

  0

  ）

  ，

  b

  =

  （

  0

  ，

  3

  ，

  4

  ）

  ，則向量

  a

  在向量

  b

  方向上的投影向量為（　　）

  A． - 9 13 a

  B． 9 13 a

  C． 9 25 b

  D． - 9 25 b
  組卷：51引用：5難度：0.8

  解析

• 3．已知直線l的方向向量為

  a

  ，平面α的法向量為

  n

  ，若

  a

  =（-1，0，-1），

  n

  =（1，0，1），則直線l與平面α（　　）

  A．垂直	B．平行
  C．相交但不垂直	D．位置關系無法確定
  組卷：84引用：3難度：0.8

  解析

• 4．下列說法正確的是（　　）

  A．經過定點P（x0，y0）的直線都可以用方程y-y0=k（x-x0）表示

  B．方程x+my-2=0（m∈R）不能表示平行y軸的直線

  C．經過點P（1，1），傾斜角為θ的直線方程為y-1=tanθ（x-1）

  D．經過兩點P1（x1，y1），P2（x2，y2）（x1≠x2）的直線方程為 y - y 1 = y 2 - y 1 x 2 - x 1 （ x - x 1 ）
  組卷：44引用：2難度：0.7

  解析

• 5．若

  {

  e

  1

  ，

  e

  2

  ，

  e

  3

  }

  是空間的一個基底，且向量

  {

  OA

  =

  e

  1

  +

  e

  2

  +

  e

  3

  ，

  OB

  =

  e

  1

  -

  2

  e

  2

  +

  2

  e

  3

  ，

  OC

  =

  k

  e

  1

  +

  3

  e

  2

  +

  2

  e

  3

  }

  不能構成空間的一個基底，則k=（　　）

  A． 8 3

  B． 5 2

  C． - 1 4

  D． 9 4
  組卷：74引用：5難度：0.6

  解析

• 6．已知直線kx-y-k-1=0和以M（-3，1），N（3，2）為端點的線段相交，則實數k的取值范圍為（　　）

  A． - 1 2 ≤ k ≤ 3 2	B． - 2 ≤ k ≤ 2 3
  C． k ≤ - 1 2 或 k ≥ 3 2	D．k≤-2或 k ≥ 2 3
  組卷：633引用：10難度：0.7

  解析

• 7．如圖，在平行六面體ABCD-A₁B₁C₁D₁中，底面是邊長為1的正方形，若∠A₁AB=∠A₁AD=60°，且AA₁=2，則AC₁的長為（　　）

  A． 5

  B． 2 2

  C． 10

  D． 15
  組卷：181引用：6難度：0.8

  解析

四、解答題。本大題共6小題，滿分70分，解答應寫出文字說明、證明過程或演算步驟．

• 21．已知空間四邊形OABC的各邊及對角線的長都相等，M，N分別是OA，BC的中點，G是MN的中點，求證：
  （1）OG⊥BC；
  （2）求異面直線ON與BM所成角的余弦值．
  組卷：53引用：2難度：0.6

  解析

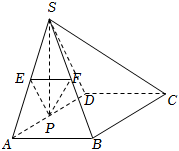• 22．如圖，在四棱錐S-ABCD中，四邊形ABCD是矩形，△SAD是等邊三角形，平面SAD⊥平面ABCD，AB=1，P為棱AD的中點，四棱錐S-ABCD的體積為

  2

  3

  3

  ．
  （1）若E為棱SA的中點，F為棱SB的中點，求證：平面PEF∥平面SCD．
  （2）在棱SA上是否存在點M，使得平面PMB與平面SAD所成銳二面角的余弦值為

  30

  10

  ？若存在，指出點M的位置；若不存在，請說明理由．
  組卷：183引用：10難度：0.6

  解析