2014-2015學年江蘇省宿遷市泗洪縣育才實驗學校八年級(下)第七次周測數學試卷
發布:2024/4/20 14:35:0
一、選擇題(每題3分,共24分)
-
1.下列說法中,不正確的是( )
A.對角線互相平分的四邊形是平行四邊形 B.兩組對角分別相等的四邊形是平行四邊形 C.一組對邊平行且相等的四邊形是平行四邊形 D.一組對邊平行另一組對邊相等的四邊形是平行四邊形 組卷:958引用:5難度:0.9 -
2.若雙曲線
的圖象經過第二、四象限,則k的取值范圍是( )y=2k-1xA. k>12B. k<12C. k=12D.不存在 組卷:241引用:21難度:0.9 -
3.甲、乙兩地相距480km,一輛汽車從甲地開往乙地,把汽車到達乙地所用時間y(h)表示為汽車平均速度x(km/h)的函數,則這個函數的圖象大致是( )
A. 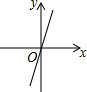
B. 
C. 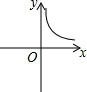
D. 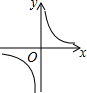 組卷:75引用:3難度:0.9
組卷:75引用:3難度:0.9 -
 4.正比例函數y=kx(k>0)與反比例函數y=的圖象相交于A、C兩點,過點A作x軸的垂線交x軸于點B,連接BC,若△ABC的面積為S,則( )1x
4.正比例函數y=kx(k>0)與反比例函數y=的圖象相交于A、C兩點,過點A作x軸的垂線交x軸于點B,連接BC,若△ABC的面積為S,則( )1xA.S=1 B.S=2 C.S=3 D.S=4 組卷:144引用:4難度:0.7 -
5.在同一坐標系中畫函數y=
和y=-kx+3的圖象,大致圖形可能是( )kxA. 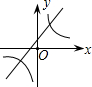
B. 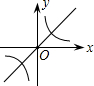
C. 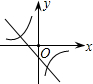
D.  組卷:654引用:6難度:0.5
組卷:654引用:6難度:0.5 -
6.若M(
,y1)、N(-12,y2)、P(-14,y3)三點都在函數12(k>0)的圖象上,則y1、y2、y3的大小關系是( )y=kxA.y2>y3>y1 B.y2>y1>y3 C.y3>y1>y2 D.y3>y2>y1 組卷:2174引用:25難度:0.9 -
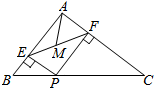 7.如圖,在△ABC中,AB=3,AC=4,BC=5,P為邊BC上一動點,PE⊥AB于E,PF⊥AC于F,M為EF中點,則AM的最小值為( )
7.如圖,在△ABC中,AB=3,AC=4,BC=5,P為邊BC上一動點,PE⊥AB于E,PF⊥AC于F,M為EF中點,則AM的最小值為( )A.1 B.1.2 C.1.3 D.1.5 組卷:1013引用:39難度:0.7 -
8.將矩形紙片ABCD按如圖所示的方式折疊,得到菱形AECF.若AB=3,則BC的長為( )

A.1 B.2 C. 2D. 3組卷:2168引用:104難度:0.9
三、解答題(17,18,19,20,21,22題各6分,23題8分,24題8分,共52分)
-
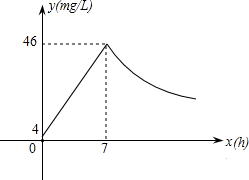 25.近年來,我國煤礦安全事故頻頻發生,其中危害最大的是瓦斯,其主要成分是CO.在一次礦難事件的調查中發現:從零時起,井內空氣中CO的濃度達到4mg/L,此后濃度呈直線型增加,在第7小時達到最高值46mg/L,發生爆炸;爆炸后,空氣中的CO濃度成反比例下降.如圖所示,根據題中相關信息回答下列問題:
25.近年來,我國煤礦安全事故頻頻發生,其中危害最大的是瓦斯,其主要成分是CO.在一次礦難事件的調查中發現:從零時起,井內空氣中CO的濃度達到4mg/L,此后濃度呈直線型增加,在第7小時達到最高值46mg/L,發生爆炸;爆炸后,空氣中的CO濃度成反比例下降.如圖所示,根據題中相關信息回答下列問題:
(1)求爆炸前后空氣中CO濃度y與時間x的函數關系式,并寫出相應的自變量取值范圍;
(2)當空氣中的CO濃度達到34mg/L時,井下3km的礦工接到自動報警信號,這時他們至少要以多少km/h的速度撤離才能在爆炸前逃生?
(3)礦工只有在空氣中的CO濃度降到4mg/L及以下時,才能回到礦井開展生產自救,求礦工至少在爆炸后多少小時才能下井?組卷:589引用:49難度:0.1 -
26.探究問題:
(1)方法感悟:
如圖①,在正方形ABCD中,點E,F分別為DC,BC邊上的點,且滿足∠EAF=45°,連接EF,求證DE+BF=EF.
感悟解題方法,并完成下列填空:
證明:延長CB到G,使BG=DE,連接AG,
∵四邊形ABCD為正方形,
∴AB=AD,∠ABC=∠D=90°,
∴∠ABG=∠D=90°,
∴△ADE≌△ABG.
∴AG=AE,∠1=∠2;
∵四邊形ABCD為正方形,
∴∠BAD=90°,
∵∠EAF=45°,
∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2,
∴∠1+∠3=45°.
即∠GAF=∠.
又AG=AE,AF=AF,
∴△GAF≌.
∴FG=EF,
∵FG=FB+BG,
又BG=DE,
∴DE+BF=EF.
變化:在圖①中,過點A作AM⊥EF于點M,請直接寫出AM和AB的數量關系 ;
(2)方法遷移: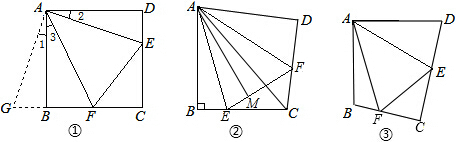
如圖②,將Rt△ABC沿斜邊AC翻折得到Rt△ADC,E,F分別是BC,CD邊上的點,∠EAF=∠BAD,連接EF,過點A作AM⊥EF于點M,試猜想DF,BE,EF之間有何數量關系,并證明你的猜想.試猜想AM與AB之間的數量關系,并證明你的猜想.12
(3)問題拓展:
如圖③,在四邊形ABCD中,AB=AD,E,F分別為DC,BC上的點,滿足∠EAF=∠DAB,試猜想當∠B與∠D滿足什么關系時,可使得DE+BF=EF.請直接寫出你的猜想(不必說明理由).猜想:∠B與∠D滿足關系:.12組卷:875引用:1難度:0.1


