2022-2023學(xué)年貴州省六校聯(lián)盟高三（上）月考數(shù)學(xué)試卷（文科）（二）

一、選擇題。（本大題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．設(shè)集合M={1，2，4}，N={n|n=2x,x∈M}，則M∪N=（　　）

  A．{2，4}

  B．{1，6}

  C．{1，2，4，8}

  D．{2，4，6}
  組卷：20引用：3難度：0.7

  解析

• 2．已知i為虛數(shù)單位，若

  1

  1

  +

  i

  =

  a

  -

  bi

  （

  a

  ,

  b

  ∈

  R

  ）

  ，則b^a=（　　）

  A．1

  B． 2 2

  C． 2

  D．2
  組卷：58引用：4難度：0.7

  解析

• 3．“一三五七八十臘，三十一天永不差；四六九冬三十整，唯有二月會變化．”月是歷法中的一種時間單位，傳統(tǒng)上都是以月相變化的周期作為一個月的長度．在舊石器時代的早期，人類就已經(jīng)會依據(jù)月相來計算日子．而星期的概念起源于巴比倫，羅馬皇帝君士坦丁大帝在公元321年宣布7天為一周，這個制度一直沿用至今，若某年某月星期一比星期三多一天，星期二和星期天一樣多，則該月3日可能是星期（　　）

  A．一或三．

  B．二或三

  C．二或五

  D．四或六
  組卷：177引用：7難度：0.7

  解析

• 4．已知曲線C的方程2x²+2y²+4x+8y+F=0，則“F≤10”是“曲線C是圓”的（　　）

  A．必要不充分條件	B．充分不必要條件
  C．充要條件	D．既不充分也不必要條件
  組卷：10引用：3難度：0.7

  解析

• 5．已知a=2^1.5，b=4^0.7，c=log₃8，則a,b,c的大小關(guān)系為（　　）

  A．a(chǎn)＜c＜b

  B．b＜c＜a

  C．c＜a＜b

  D．c＜b＜a
  組卷：38引用：2難度：0.7

  解析

• 6．函數(shù)

  y

  =

  |

  x

  |

  ln

  1

  +

  x

  1

  -

  x

  在（-1，1）上的圖象大致為（　　）

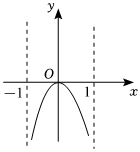
  A．	B．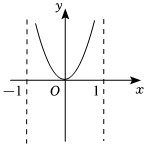
  C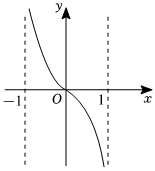．	D．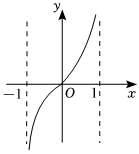
  組卷：38引用：4難度：0.7

  解析

• 7．如圖甲是一個不倒翁模型，它是一種古老的中國兒童玩具，最早記載出現(xiàn)于唐代，一經(jīng)觸動就搖擺，然后恢復(fù)直立狀態(tài)，將圖甲的模型抽象成一個圓錐和半球的組合體，如圖乙，已知不倒翁在一定角度范圍內(nèi)“不倒”，那么模型中半球的質(zhì)量應(yīng)不小于圓錐質(zhì)量，若半球的密度是圓錐的2倍，則圓錐的高與底面半徑之比至多為（　　）

  A．4

  B．2

  C．1

  D． 1 2
  組卷：13引用：3難度：0.7

  解析

請考生在第22、23兩題中任選一題作答，并用2B鉛筆在答題卡上把所選題目的題號涂黑．注意所做題目的題號必須與所涂題目的題號一致，在答題卡選答區(qū)域指定位置答題．如果多做，則按所做的第一題計分．【選修4-4：坐標(biāo)系與參數(shù)方程】

• 22．在平面直角坐標(biāo)系xOy中，已知曲線C的參數(shù)方程為

  x = - 1 + 2 cosθ

  y = 1 + 2 sinθ

  （θ為參數(shù)），以原點O為極點，x軸正半軸為極軸建立極坐標(biāo)系．
  （1）求曲線C的極坐標(biāo)方程；
  （2）設(shè)射線l₁：θ=π（ρ≥0）和射線

  l

  2

  ：

  θ

  =

  π

  2

  +

  α

  （

  ρ

  ≥

  0

  ，

  0

  ≤

  α

  ≤

  π

  2

  ）

  分別與曲線C交于A，B兩點，求△AOB面積的最大值．
  組卷：211引用：9難度：0.7

  解析

【選修4-5：不等式選講】

• 23．已知△ABC對應(yīng)的三邊分別為a,b,c.
  （1）若x,y,z是正實數(shù)，求證：

  a

  2

  x

  +

  b

  2

  y

  +

  c

  2

  z

  ≥

  （

  a

  +

  b

  +

  c

  ）

  2

  x

  +

  y

  +

  z

  ，當(dāng)

  a

  x

  =

  b

  y

  =

  c

  z

  時，等號成立；
  （2）求證：

  c

  a

  +

  b

  +

  a

  b

  +

  c

  +

  b

  c

  +

  a

  ≥

  3

  2

  ．
  組卷：35引用：4難度：0.5

  解析