2022-2023學年安徽省十校聯盟高二（下）開學數學試卷

一、選擇題（本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的.）

• 1．橢圓

  x

  2

  15

  +

  y

  2

  25

  =

  1

  的焦點坐標是（　　）

  A． （ 0 ， ± 10 ）

  B．（0，±10）

  C． （ ± 10 ， 0 ）

  D．（±10，0）
  組卷：213引用：1難度：0.9

  解析

• 2．若直線l₁：x-4y-3=0與直線l₂：3x-my+1=0（m∈R）互相垂直，則m=（　　）

  A． 3 4

  B． - 3 4

  C．12

  D．-12
  組卷：43引用：2難度：0.8

  解析

• 3．直線l：ax+y-a=2與圓C：（x-2）²+（y-1）²=4的位置關系為（　　）

  A．相交	B．相切
  C．相離	D．與a的值有關
  組卷：53引用：1難度：0.7

  解析

• 4．定義：對于數列{a_n}，如果存在一個常數T（T∈N^*），使得對任意的正整數n≥n₀恒有a_n+T=a_n，則稱數列{a_n}是從第n₀項起的周期為T的周期數列．已知周期數列{b_n}滿足：b₁=1，b₂=3，b_n=b_n-1-b_n-2（n≥3），則b₂₀₂₃=（　　）

  A．-1

  B．-3

  C．-2

  D．1
  組卷：80引用：1難度：0.8

  解析

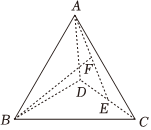• 5．在正四面體ABCD中，E是CD的中點，F是AE的中點，若

  AB

  =

  a

  ，

  AC

  =

  b

  ，

  AD

  =

  c

  ，則

  BF

  =（　　）

  A． 1 2 a - b + 1 2 c

  B． a + 1 4 b - 1 4 c

  C． - a + 1 4 b + 1 4 c

  D． 1 4 a - b + 1 4 c
  組卷：233引用：3難度：0.9

  解析

• 6．已知O為坐標原點，P是焦點為F的拋物線C：y²=2px（p＞0）上一點，|PF|=2，

  ∠

  PFO

  =

  π

  3

  ，則p=（　　）

  A．1

  B． 3 2

  C．2

  D．3
  組卷：32引用：1難度：0.7

  解析

• 7．已知雙曲線

  x

  2

  9

  -

  y

  2

  b

  2

  =

  1

  （b＞0）上的點A，B關于原點對稱，點P在雙曲線上（異于點A，B），直線PA，PB的斜率滿足k_PA?k_PB=2，則b=（　　）

  A．2

  B． 2 3

  C． 3 2

  D．3
  組卷：43引用：1難度：0.6

  解析

四、解答題（本題共6小題，第17題10分，第18～22題每題12分，共70分．解答應寫出文字說明、證明過程或演算步驟．）

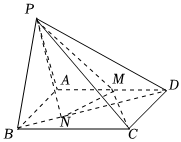• 21．如圖，四棱錐P-ABCD的底面ABCD為正方形，二面角P-AB-D為直二面角，∠PAB=∠PBA，點M為棱AD的中點．
  （1）求證：PD⊥MC；
  （2）若PA=AB，點N是線段BD上靠近B的三等分點，求直線PA與平面PMN所成角的正弦值．
  組卷：32引用：1難度：0.5

  解析

• 22．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （a＞b＞0）的離心率為

  2

  2

  ，且過點

  （

  2

  ，

  6

  ）

  ．
  （1）求C的標準方程；
  （2）過C的左焦點且斜率為k（k≠0）的直線l與C交于A，B兩點，O為坐標原點，當△OAB的面積為

  16

  3

  時，求k的值．
  組卷：154引用：3難度：0.7

  解析