2013-2014學年山東省高二（下）暑假數(shù)學作業(yè)（3）

一、選擇題

• 1．“x²-2x＜0”是“|x-2|＜2”的（　　）

  A．充分條件	B．充分而不必要條件
  C．必要而不充分條件	D．既不充分也不必要條件
  組卷：6引用：7難度：0.9

  解析

• 2．已知等差數(shù)列{a_n}的首項為a₁，公差為d,其前n項和為S_n，若直線y=a₁x與圓（x-2）²+y²=1的兩個交點關(guān)于直線x+y+d=0對稱，則S_n=（　　）

  A．n2

  B．-n2

  C．2n-n2

  D．n2-2n
  組卷：38引用：7難度：0.9

  解析

• 3．曲線

  x = - 2 + 3 λ 1 + λ

  y = 1 - λ 1 + λ

  （λ為參數(shù)）與y坐標軸的交點是（　　）

  A．（0， 2 5 ）

  B．（0， 1 5 ）

  C．（0，-4）

  D．（0， 5 9 ）
  組卷：102引用：8難度：0.7

  解析

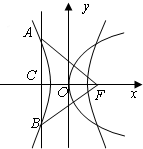• 4．已知拋物線y²=4x的準線與雙曲線

  x

  2

  a

  2

  -

  y

  2

  =

  1

  交于A、B兩點，點F為拋物線的焦點，若△FAB為直角三角形，則雙曲線的離心率為（　　）

  A． 6

  B． 6 2

  C． 3

  D．2
  組卷：127引用：15難度：0.9

  解析

• 5．已知雙曲線

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1的一個焦點與拋物線y²=4x的焦點重合，且雙曲線的離心率等于

  5

  ，則該雙曲線的方程為（　　）

  A． 5 x 2 - 4 5 y 2 = 1

  B． x 2 5 - y 2 4 = 1

  C． y 2 5 - x 2 4 = 1

  D． 5 x 2 - 5 4 y 2 = 1
  組卷：1369引用：77難度：0.9

  解析

三、解答題

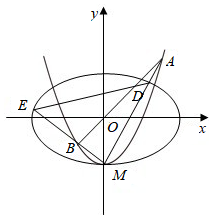• 16．如圖，橢圓

  C

  1

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的離心率為

  2

  2

  ，x軸被曲線

  C

  2

  ：

  y

  =

  x

  2

  -

  b

  截得的線段長等于C₁的短軸長．C₂與y軸的交點為M，過坐標原點O的直線l與C₂相交于點A、B，直線MA，MB分別與C₁相交于點D、E．
  （1）求C₁、C₂的方程；
  （2）求證：MA⊥MB．
  （3）記△MAB，△MDE的面積分別為S₁、S₂，若

  S

  1

  S

  2

  =

  λ

  ，求λ的取值范圍．
  組卷：72引用：11難度：0.5

  解析

• 17．已知數(shù)列{a_n}是等差數(shù)列，c_n=a_n²-a_n+1²（n∈N^*）
  （1）判斷數(shù)列{c_n}是否是等差數(shù)列，并說明理由；
  （2）如果a₁+a₃+…+a₂₅=130，a₂+a₄+…+a₂₆=143-13k（k為常數(shù)），試寫出數(shù)列{c_n}的通項公式；
  （3）在（2）的條件下，若數(shù)列{c_n}得前n項和為S_n，問是否存在這樣的實數(shù)k,使S_n當且僅當n=12時取得最大值．若存在，求出k的取值范圍；若不存在，說明理由．
  組卷：232引用：10難度：0.1

  解析