2022-2023學年北京五中高二（下）期末數學試卷

一、單選題（每小題4分，共40分）

• 1．已知集合A={x|1＜x＜3}，B={x|x≤2}，那么集合A∩B等于（　　）

  A．{x|1＜x＜2}

  B．{x|2＜x＜3}

  C．{x|1＜x≤2}

  D．{x|2≤x＜3}
  組卷：24引用：4難度：0.9

  解析

• 2．若復數z滿足i?z=3-4i,則|z|=（　　）

  A． 10

  B．5

  C．7

  D．25
  組卷：116引用：3難度：0.8

  解析

• 3．（x-2y）⁴的展開式中含x²y²的項的系數為（　　）

  A．24

  B．-24

  C．6

  D．-6
  組卷：163引用：3難度：0.8

  解析

• 4．關于向量

  a

  ，

  b

  ，

  c

  ，下列命題中正確的是（　　）

  A．若 | a | = | b | ，則 a = b	B．若 a = - b ，則 a ∥ b
  C．若 a ∥ b ， b ∥ c ，則 a ∥ c	D．若 | a | ＞ | b | ，則 a ＞ b
  組卷：395引用：6難度：0.8

  解析

• 5．布達佩斯的伊帕姆維澤蒂博物館收藏的達?芬奇方磚，在正六邊形上畫了具有視覺效果的正方體圖案（如圖1），把三片這樣的達?芬奇方磚形成圖2的組合，這個組合表達了圖3所示的幾何體．如圖3中每個正方體的棱長為1，則點A到平面QGC的距離是（　　）

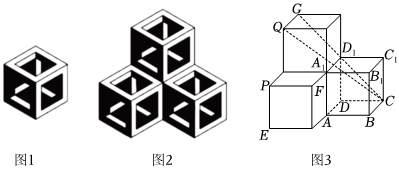
  A． 1 4

  B． 1 2

  C． 2 2

  D． 3 2
  組卷：187引用：10難度：0.5

  解析

• 6．點F是拋物線x²=8y的焦點，A為雙曲線C：

  x

  2

  8

  -

  y

  2

  b

  =

  1

  的左頂點，直線AF平行于雙曲線C的一條漸近線，則實數b的值為（　　）

  A．2

  B．4

  C．8

  D．16
  組卷：623引用：7難度：0.5

  解析

• 7．在△ABC中，角A，B，C所對的邊分別為a,b,c,∠A=60°，且△ABC的面積為

  3

  ，若b+c=6，則a=（　　）

  A． 2 6

  B．5

  C． 30

  D． 2 7
  組卷：313引用：8難度：0.6

  解析

三、解答原（第16-19、21題14分，第20題15分）

• 20．已知函數f（x）=e^x，g（x）=ln（x+a）（a∈R）．
  （1）求曲線y=f（x）在點（1，f（1））處的切線方程；
  （2）設φ（x）=f（x）g（x），請判斷φ（x）是否存在極值？若存在，求出極值；若不存在，說明理由；
  （3）當a=0時，若對于任意s＞t＞0，不等式

  g

  （

  s

  ）

  -

  g

  （

  t

  ）

  ＞

  k

  （

  1

  f

  （

  s

  ）

  -

  1

  f

  （

  t

  ）

  ）

  恒成立，求k的取值范圍．
  組卷：717引用：4難度：0.3

  解析

• 21．已知各項均為整數的數列A_N：a₁，a₂，…，a_N（N≥3，N∈N*）滿足a₁a_N＜0，且對任意i=2，3，…，N，都有|a_i-a_i-1|≤1．記S（A_N）=a₁+a₂+…+a_N．
  （Ⅰ）若a₁=3，寫出一個符合要求的A₆；
  （Ⅱ）證明：數列A_N中存在a_k使得a_k=0；
  （Ⅲ）若S（A_N）是N的整數倍，證明：數列A_N中存在a_r，使得S（A_N）=N?a_r．
  組卷：226引用：6難度：0.2

  解析