2023年陜西省渭南市高考數學二模試卷（文科）

一、選擇題：本大題共12小題，每小題5分，共60分.

• 1．已知集合

  A

  =

  {

  x

  |

  y

  =

  2

  -

  x

  }

  ，

  B

  =

  {

  x

  |

  lo

  g

  2

  x

  ＜

  1

  }

  ，則A∩B=（　　）

  A．（-∞，2）

  B．（0，2）

  C．（-∞，2]

  D．（0，2]
  組卷：43引用：3難度：0.7

  解析

• 2．已知平面向量

  a

  ，

  b

  滿足

  |

  a

  |

  =

  4

  ，

  |

  b

  |

  =

  2

  ，

  a

  ?

  （

  a

  -

  b

  ）

  =

  20

  ，則向量

  a

  與

  b

  的夾角為（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 5 π 6
  組卷：324引用：11難度：0.7

  解析

• 3．函數f（x）=xcosx的部分圖象大致為（　　）

  A．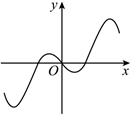

  B．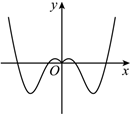

  C．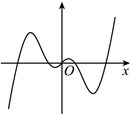

  D．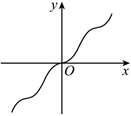
  組卷：144引用：4難度：0.8

  解析

• 4．棣莫弗公式（cosθ+isinθ）ⁿ=cosnθ+isinnθ（i為虛數單位）是由法國數學家棣莫弗（1667-1754）發現的．若復數z滿足

  z

  ?

  （

  cos

  π

  8

  +

  i

  ?

  sin

  π

  8

  ）

  =

  |

  1

  +

  i

  |

  ，復數z對應的點在復平面內的（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：35引用：4難度：0.8

  解析

• 5．已知命題p：?x＜1，log₃x＞0；命題

  q

  ：

  ?

  x

  0

  ∈

  R

  ，

  x

  2

  0

  ≥

  2

  x

  0

  ，則下列命題中為真命題的是（　　）

  A．p∨q

  B．（?p）∧（?q）

  C．p∨（?q）

  D．p∧q
  組卷：24引用：1難度：0.8

  解析

• 6．已知sinθ+2cos²

  θ

  2

  =

  5

  4

  ，則sin2θ=（　　）

  A． - 15 16

  B． 15 16

  C． - 3 4

  D． 3 4
  組卷：536引用：9難度：0.8

  解析

• 7．將拋物線y²=mx繞其頂點順時針旋轉90°之后，正好與拋物線y=2x²重合，則m=（　　）

  A． - 1 2

  B． 1 2

  C．-2

  D．2
  組卷：49引用：4難度：0.7

  解析

選修4-4：坐標系與參數方程

• 22．在直角坐標系xOy中，曲線C的參數方程為

  x = 1 cosα ，

  y = 3 sinα cosα ，

  （α為參數，

  α

  ≠

  kπ

  +

  π

  2

  ），以坐標原點O為極點，x軸的非負半軸為極軸建立極坐標系，直線l的極坐標方程為

  ρcos

  （

  θ

  +

  π

  3

  ）

  =

  1

  ．
  （1）求曲線C的普通方程和直線l的直角坐標方程；
  （2）已知點P（2，0），若直線l與曲線C交于A，B兩點，求

  |

  1

  |

  PA

  |

  -

  1

  |

  PB

  |

  |

  的值．
  組卷：306引用：12難度：0.5

  解析

選修4-5：不等式選講

• 23．已知函數f（x）=|x+a|+2|x-1|．
  （1）當a=1時，求f（x）的最小值；
  （2）若a＞0，b＞0時，對任意x∈[1，2]，使得不等式f（x）＞x²-b+1恒成立，證明：（a+

  1

  2

  ）²+（b+

  1

  2

  ）²＞2．
  組卷：44引用：13難度：0.6

  解析