2023-2024學年廣東省廣州市海珠外國語實驗中學八年級(上)期中數學試卷
發布:2024/10/8 18:0:9
一、單選題:本大題10小題,每小題3分,共30分。
-
1.下面四個圖形分別是節能、節水、低碳和綠色食品標志,在這四個標志中,是軸對稱圖形的是( )
A. 
B. 
C. 
D.  組卷:1748引用:75難度:0.9
組卷:1748引用:75難度:0.9 -
2.已知三角形的兩邊長分別為1和4,第三邊長為整數,則該三角形的周長為( )
A.7 B.8 C.9 D.10 組卷:3537引用:54難度:0.8 -
3.如圖,四個圖形中,線段BE是△ABC的高的圖是( )
A. 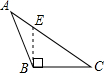
B. 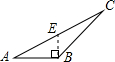
C. 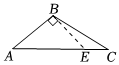
D. 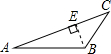 組卷:9392引用:76難度:0.9
組卷:9392引用:76難度:0.9 -
 4.一副直角三角板如圖放置,點C在FD的延長線上,AB∥CF,∠F=∠ACB=90°,則∠DBC的度數為( )
4.一副直角三角板如圖放置,點C在FD的延長線上,AB∥CF,∠F=∠ACB=90°,則∠DBC的度數為( )A.15° B.18° C.25° D.30° 組卷:914引用:12難度:0.7 -
 5.如圖,AD是△ABC邊上的中線,CE是AB邊上的高,AB=6,S△ADC=6,CE=( )
5.如圖,AD是△ABC邊上的中線,CE是AB邊上的高,AB=6,S△ADC=6,CE=( )A.3 B.4 C.5 D.6 組卷:73引用:1難度:0.5 -
 6.如圖,△ABC≌△ADE,D在BC邊上,∠E=35°,∠DAC=30°,則∠BDA的度數為( )
6.如圖,△ABC≌△ADE,D在BC邊上,∠E=35°,∠DAC=30°,則∠BDA的度數為( )A.35° B.40° C.50° D.65° 組卷:994引用:7難度:0.7 -
 7.如圖,△ABC為直角三角形,∠C=90°,若沿圖中虛線剪去∠C,則∠1+∠2等于( )
7.如圖,△ABC為直角三角形,∠C=90°,若沿圖中虛線剪去∠C,則∠1+∠2等于( )A.90° B.135° C.150° D.270° 組卷:1209引用:3難度:0.7 -
 8.如圖,在△ABC中,AB=AC,∠BAC=120°,點D在BC上,AB⊥AD,AD=2cm,則BC的長為( )
8.如圖,在△ABC中,AB=AC,∠BAC=120°,點D在BC上,AB⊥AD,AD=2cm,則BC的長為( )A.4cm B.5cm C.6cm D.8cm 組卷:778引用:10難度:0.5
三.解答題:共72分。
-
24.【問題背景】
在四邊形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分別是BC、CD上的點,且∠EAF=60°,試探究圖1中線段BE、EF、FD之間的數量關系.
【初步探索】
小亮同學認為:延長FD到點G,使DG=BE,連接AG,先證明△ABE≌△ADG,再證明△AEF≌△AGF,則可得到BE、EF、FD之間的數量關系是 .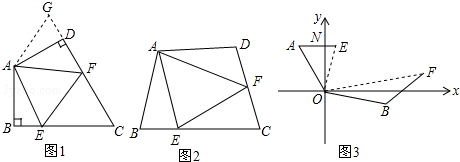
【探索延伸】
在四邊形ABCD中如圖2,AB=AD,∠B+∠D=180°,E、F分別是BC、CD上的點,∠EAF=∠BAD,上述結論是否仍然成立?說明理由.12
【結論運用】
如圖3,在某次軍事演習中,艦艇甲在指揮中心(O處)北偏西30°的A處,艦艇乙在指揮中心南偏東70°的B處,并且兩艦艇到指揮中心的距離相等,接到行動指令后,艦艇甲向正東方向以60海里/小時的速度前進,艦艇乙沿北偏東50°的方向以80海里/小時的速度前進1.5小時后,指揮中心觀測到甲、乙兩艦艇分別到達E,F處,且兩艦艇之間的夾角(∠EOF)為70°,試求此時兩艦艇之間的距離.組卷:6736引用:38難度:0.3 -
25.在長方形ABCD中,AB=4,BC=8,點P、Q為BC邊上的兩個動點(點P位于點Q的左側,P、Q均不與頂點重合),PQ=2.
(1)如圖①,若點E為CD邊上的中點,當Q移動到BC邊上的中點時,求證:AP=QE;
(2)如圖②,若點E為CD邊上的中點,在PQ的移動過程中,若四邊形APQE的周長最小時,求BP的長;
(3)如圖③,若M、N分別為AD邊和CD邊上的兩個動點(M、N均不與頂點重合),當BP=3,且四邊形PQNM的周長最小時,求此時四邊形PQNM的面積. 組卷:871引用:2難度:0.3
組卷:871引用:2難度:0.3


