2022-2023學年浙江省名校協作體高二（下）月考數學試卷

一、單選題：本大題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的

• 1．已知A（1，-2，3），則點A關于xOy平面的對稱點的坐標是（　　）

  A．（-1，-2，3）

  B．（-1，-2，-3）

  C．（1，-2，-3）

  D．（-1，2，-3）
  組卷：59引用：2難度：0.7

  解析

• 2．與雙曲線

  x

  2

  4

  -

  y

  2

  =

  1

  有公共焦點，且長軸長為6的橢圓方程為（　　）

  A． x 2 9 + y 2 4 = 1

  B． x 2 4 + y 2 9 = 1

  C． x 2 9 + y 2 6 = 1

  D． x 2 6 + y 2 9 = 1
  組卷：49引用：3難度：0.7

  解析

• 3．在數列{a_n}中，a₄=25，

  a

  n

  +

  1

  =

  a

  n

  +2，則a₆=（　　）

  A．121

  B．64

  C．100

  D．81
  組卷：287引用：3難度：0.6

  解析

• 4．直線ax+y-a=0（a∈R）與圓（x-2）²+y²=4的位置關系是（　　）

  A．相離

  B．相交

  C．相切

  D．無法確定
  組卷：16引用：3難度：0.7

  解析

• 5．正項等比數列{a_n}公比為q,前n項和S_n，則“q＞1”是“S₂₀₂₁+S₂₀₂₃＞2S₂₀₂₂”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：89引用：2難度：0.6

  解析

• 6．已知拋物線y²=2px,點A（1，2）在拋物線上，斜率為1的直線交拋物線于B、C兩點．直線AB、AC的斜率分別記為k₁，k₂，則

  1

  k

  1

  +

  1

  k

  2

  的值為（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：60引用：1難度：0.7

  解析

• 7．已知長方體ABCD-A₁B₁C₁D₁，其中AA₁=

  2

  ，AB=AD=

  3

  ，P為底面ABCD上的動點，PE⊥A₁C于E，且PA=PE，設A₁P與平面ABCD所成的角為θ，則θ的最大值為（　　）

  A． π 4

  B． π 2

  C． π 6

  D． π 3
  組卷：409引用：1難度：0.3

  解析

四、解答題：本大題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

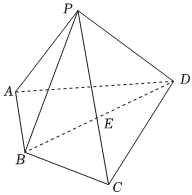• 21．如圖所示，已知四棱錐P-ABCD，滿足E為BD中點，∠BAD=∠BCD=90°，AD=

  3

  AB，PA=PB=PD．
  （Ⅰ）求證PE⊥平面ABCD；
  （Ⅱ）若PA與BD夾角的余弦值為

  2

  4

  ，且CE∥AB，求PC與平面PAD夾角的正弦值．
  組卷：141引用：2難度：0.4

  解析

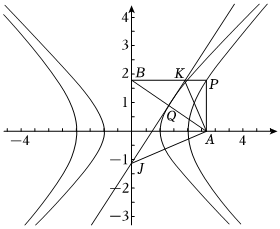• 22．已知雙曲線E：x²-y²=1，雙曲線C與E共漸近線且經過點

  （

  -

  5

  ，

  1

  ）

  ．
  （Ⅰ）求雙曲線C的標準方程．
  （Ⅱ）如圖所示，點P是曲線C上任意一動點（第一象限），直線PA⊥x軸于點A，PB⊥y軸于點B，直線AB交曲線E于點Q（第一象限），過點Q作曲線E的切線交PB于點K，交y軸于點J，求S_△KQA+S_△BQJ的最小值．
  組卷：15引用：2難度：0.6

  解析