當前位置：試卷中心 > 試卷詳情

2023-2024學年江蘇省南京市六校聯合體高二（上）段考數學試卷（10月份）

發布：2024/9/23 15:0:8

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．若直線l過點（0，1），（
3
，
4
）
，則該直線的傾斜角為（　　）
A．30° B．60° C．120° D．150°
組卷：51引用：1難度：0.8
解析
2．若z（1+i）=1-i,則z等于（　　）
A．1-i B．1+i C．-i D．i
組卷：44引用：1難度：0.7
解析
3．已知向量
a
=
（
-
1
，
2
）
，
b
=
（
2
，
m
）
，若
a
⊥
b
，則m=（　　）
A．-1 B．1 C．
-
1
4
D．
1
4
組卷：172引用：6難度：0.9
解析
4．已知α∈（0，π），且3cos2α-8cosα=5，則sinα=（　　）
A．
5
3
B．
2
3
C．
1
3
D．
5
9
組卷：9506引用：39難度：0.7
解析
5．已知a,b為兩條不同的直線，α，β，γ為三個不同的平面，則下列說法正確的是（　　）
A．若a∥b,b?α，則a∥α
B．若a?α，b?β，a∥b,則α∥β
C．若α⊥β，α∩β=a,a⊥b,則b⊥α
D．α∩β=a,β∩γ=b,α∩γ=c,a∥b,則b∥c
組卷：46引用：1難度：0.7
解析
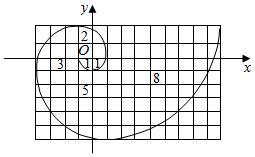6．人教A版選擇性必修二教材的封面圖案是斐波那契螺旋線，它被譽為自然界最完美的“黃金螺旋”，自然界存在很多斐波那契螺旋線的圖案，例如向日葵、鸚鵡螺等．斐波那契螺旋線的畫法是：以斐波那契數1，1，2，3，5，8，…為邊長的正方形拼成長方形，然后在每個正方形中畫一個圓心角為90°的圓弧，這些圓弧所連起來的弧線就是斐波那契螺旋線．如圖為該螺旋線在正方形邊長為1，1，2，3，5，8的部分，如圖建立平面直角坐標系（規定小方格的邊長為1），則接下來的一段圓弧所在圓的方程為（　　）
A．x²+y²=144 B．（x-1）²+（y-2）²=144
C．（x+4）²+（y-2）²=169 D．（x-4）²+（y+2）²=169
組卷：297引用：8難度：0.8
解析
7．已知F₁，F₂分別為橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的左、右焦點，A是橢圓C的左頂點，點P在過A且斜率為
3
4
的直線上，△PF₁F₂為等腰三角形，∠F₁F₂P=120°，則橢圓C的離心率為（　　）
A．
1
4
B．
1
3
C．
1
2
D．
2
3
組卷：932引用：7難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

21．已知雙曲線C：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的左、右焦點分別為F₁，F₂，雙曲線C的右頂點A在圓O：x²+y²=1上，且
A
F
1
?
A
F
2
=
-
3
．
（1）求雙曲線C的標準方程；
（2）動直線l與雙曲線C恰有1個公共點，且與雙曲線C的兩條漸近線分別交于點M，N，求△OMN（O為坐標原點）的面積．
組卷：133引用：1難度：0.4
解析
22．已知橢圓C：
x
2
a
2
+
y
2
b
2
=
1
（a＞b＞0）過點A（2，1），離心率為
3
2
．
（1）求橢圓C的標準方程；
（2）設點A關于y軸的對稱點為B，直線l與OA平行，且與橢圓C相交于M，N兩點，直線AM，AN分別與y軸交于P，Q兩點．求證：四邊形APBQ為菱形．
組卷：559引用：3難度：0.6
解析