當前位置：試卷中心 > 試卷詳情

2021-2022學年廣東省茂名市化州市高一（下）期中數學試卷

發布：2024/11/28 19:30:2

1．已知集合A={x|2x+1＞3}，B={x|x²-x-2＜0}，則A∩B=（　　）
A．{x|x＞-1} B．{x|-1＜x＜1}
C．{x|-2＜x＜1或x＞1} D．{x|1＜x＜2}
組卷：44引用：3難度：0.9
解析
2．已知復數z=a+bi（a,b∈R），若
a
i
2021
+2=b+i,則z=（　　）
A．-1+2i B．1+2i C．-1-2i D．1-2i
組卷：144引用：2難度：0.7
解析
3．不等式“
（
1
2
）
x
＜
2
”是“log₂x＞1”成立的（　　）
A．充分不必要條件 B．必要不充分條件
C．充要條件 D．既不充分也不必要條件
組卷：144引用：5難度：0.8
解析
4．函數
f
（
x
）
=
sinx
+
2
x
cosx
+
x
2
在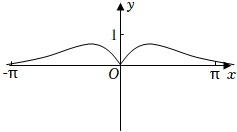[-π，π]上的圖象大致為（　　）
A． B．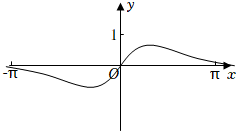
C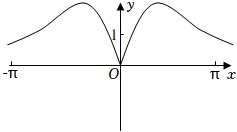． D．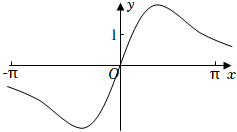
組卷：73引用：5難度：0.7
解析
5．如圖，在△ABC中，
AN
=
1
2
NC
，P是BN上的一點，若
AP
=（m+
1
3
）
AB
+
1
9
AC
，則實數m的值為（　　）
A．
1
9
B．
2
9
C．
2
3
D．
1
3
組卷：640引用：6難度：0.8
解析
6．已知正方體ABCD-A₁B₁C₁D₁中，E，F分別是它們所在線段的中點，則滿足A₁F∥平面BD₁E的圖形個數為（　　）
A．0 B．1 C．2 D．3
組卷：1178引用：12難度：0.6
解析
7．已知向量
a
=（sinθ，-3），
b
=（1，cosθ），且
a
⊥
b
，則sin2θ+cos²θ的值為（　　）
A．
7
10
B．
10
7
C．
3
2
D．
2
3
組卷：129引用：3難度：0.7
解析

21．新冠肺炎期間，呼吸機成為緊缺設備，某企業在國家科技的支持下，進行設備升級，生產了一批新型的呼吸機．已知該種設備年固定研發成本為60萬元，每生產一臺需另投入100元，設該公司一年內生產該設備x萬臺，且全部售完，由于產能原因，該設備產能最多為32萬臺，且每萬臺的銷售收入f（x）（單位：萬元）與年產量x（單位：萬臺）的函數關系式近似滿足：
f
（
x
）
=
180
-
2
x
,
0
＜
x
≤
18
70
+
2650
x
-
27000
x
2
，
18
＜
x
≤
32
．
（1）寫出年利潤W（x）（萬元）關于年產量x（萬臺）的函數解析式．（年利潤=年銷售收入-總成本）；
（2）當年產量為多少萬臺時，該公司獲得的利潤最大？
組卷：87引用：5難度：0.7
解析
22．已知二次函數f（x）=x²-2mx-3，關于x的不等式f（x）≤0的解集為[-1，n]．
（1）求函數f（x）在[-2，2]上的最大值；
（2）若不等式f（2^x）-（a²-a）?2^x+19≥0對任意的x∈[1，3]恒成立，求實數a的取值范圍．
組卷：378引用：4難度：0.3
解析

A．{x\|x＞-1}	B．{x\|-1＜x＜1}
C．{x\|-2＜x＜1或x＞1}	D．{x\|1＜x＜2}

A．充分不必要條件	B．必要不充分條件
C．充要條件	D．既不充分也不必要條件

A．	B．
C．	D．

1．已知集合A={x|2x+1＞3}，B={x|x2-x-2＜0}，則A∩B=（ ）