2023年廣東省深圳市高考數學沖刺試卷（一）（4月份）

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．已知集合

  A

  =

  {

  0

  ，

  1

  ，

  2

  ，

  3

  ，

  4

  }

  ，

  B

  =

  {

  x

  |

  1

  9

  ≤

  （

  1

  3

  ）

  x

  ≤

  1

  ，

  x

  ∈

  Z

  }

  ，則A∩B=（　　）

  A．{0，2}

  B．{1，2}

  C．{0，1，2}

  D．{1，2，4}
  組卷：182引用：4難度：0.8

  解析

• 2．已知復數z滿足

  z

  -

  i

  =

  -

  2

  1

  +

  i

  ，則z在復平面內所對應的點位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：200引用：4難度：0.9

  解析

• 3．圓錐側面展開圖扇形的圓心角為60°，底面圓的半徑為8，則圓錐的側面積為（　　）

  A．384π

  B．392π

  C．398π

  D．404π
  組卷：358引用：6難度：0.7

  解析

• 4．已知

  cos

  2

  x

  =

  -

  1

  3

  ，則

  co

  s

  2

  （

  x

  -

  π

  6

  ）

  +

  co

  s

  2

  （

  x

  +

  π

  6

  ）

  的值為（　　）

  A． 9 16

  B． 5 6

  C． 13 20

  D． 17 24
  組卷：388引用：4難度：0.7

  解析

• 5．某班學生的一次的數學考試成績ξ（滿分：100分）服從正態分布：ξ～N（85，σ²），且P（83＜ξ＜87）=0.3，P（78＜ξ＜83）=0.12，P（ξ≤78）=（　　）

  A．0.14

  B．0.18

  C．0.23

  D．0.26
  組卷：518引用：6難度：0.8

  解析

• 6．已知雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的左、右焦點分別為F₁，F₂，過F₂的直線與C的左、右兩支分別交于A，B兩點，|AF₁|+|AF₂|=24，|AF₁|=|BF₁|=5λ，|AB|=4λ，則實數λ=（　　）

  A． 1 4

  B． 1 2

  C．2

  D．4
  組卷：148引用：4難度：0.6

  解析

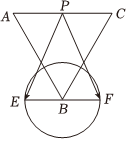• 7．如圖所示，△ABC是邊長為8的等邊三角形，P為AC邊上的一個動點，EF是以B為圓心，3為半徑的圓的直徑，則

  PE

  ?

  PF

  的取值范圍是（　　）

  A．[28，46]

  B．[32，58]

  C．[39，55]

  D．[42，60]
  組卷：215引用：2難度：0.6

  解析

四、解答題：本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

• 21．已知斜率存在的直線l過點P（1，0）且與拋物線C：y²=2px（p＞0）交于A，B兩點．
  （1）若直線l的斜率為1，M為線段AB的中點，M的縱坐標為2，求拋物線C的方程；
  （2）若點Q也在x軸上，且不同于點P，直線AQ，BQ的斜率滿足k_AQ+k_BQ=0，求點Q的坐標．
  組卷：310引用：5難度：0.4

  解析

• 22．已知函數f（x）=xe^x+ax²（a∈R）．
  （1）當

  a

  =

  -

  1

  2

  時，求曲線y=f（x）在點（1，f（1））處的切線方程；
  （2）若函數g（x）=xlnx+xe^x-f（x）有兩個極值點，求實數a的取值范圍．
  組卷：209引用：2難度：0.5

  解析