2020-2021學(xué)年重慶八中八年級(jí)（下）第三次定時(shí)訓(xùn)練數(shù)學(xué)試卷

一、選擇題（本大題共10小題，每小題4分，共40分）在每個(gè)小題的下面，都給出了代號(hào)為A、B、C、D的四個(gè)答案，請(qǐng)將答題卡上對(duì)應(yīng)選項(xiàng)的代號(hào)涂黑.

• 1．如圖所示的幾何圖形中，既是軸對(duì)稱(chēng)圖形又是中心對(duì)稱(chēng)圖形的個(gè)數(shù)是（　　）
  

  A．4

  B．3

  C．2

  D．1
  組卷：264引用：69難度：0.9

  解析

• 2．運(yùn)用分式的性質(zhì)，下列計(jì)算正確的是（　　）

  A． - x + y 2 = - x + y 2	B． x - 3 x 2 - 9 = 1 x - 3
  C． x 2 - 2 xy + y 2 x - y = x - y	D． xy x 2 - xy = x x - y
  組卷：702引用：4難度：0.8

  解析

• 3．下列從左到右的變形中，屬于因式分解的是（　　）

  A．（x+2）（x-2）=x2-4

  B．a(chǎn)2-2ab+b2=（a-b）2

  C．a(chǎn)m+bm-1=m（a+b）-1

  D．（x-1）2-1=（x-1）（x-1- 1 x - 1 ）
  組卷：1051引用：5難度：0.8

  解析

• 4．下列關(guān)于判定平行四邊形的說(shuō)法錯(cuò)誤的是（　　）

  A．一組對(duì)角相等且一組對(duì)邊平行的四邊形

  B．一組對(duì)邊相等且另一組對(duì)邊平行的四邊形

  C．兩組對(duì)角分別相等的四邊形

  D．四條邊相等的四邊形
  組卷：976引用：8難度：0.7

  解析

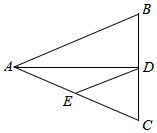• 5．如圖，△ABC中，AB=AC=12，BC=10，AD平分∠BAC交BC于點(diǎn)D，點(diǎn)E為AC的中點(diǎn)，連接DE，則△CDE的周長(zhǎng)為（　　）

  A．11

  B．17

  C．18

  D．16
  組卷：463引用：6難度：0.7

  解析

• 6．某新能源環(huán)保汽車(chē)去年第四季度銷(xiāo)售總額為2000萬(wàn)元，由于受全球經(jīng)濟(jì)下行壓力的影響，今年第一季度每輛車(chē)的銷(xiāo)售價(jià)格比去年降低1萬(wàn)元，銷(xiāo)售數(shù)量與去年第四季度相同，銷(xiāo)售總額比去年第四季度減少20%，今年第一季度每輛車(chē)的銷(xiāo)售價(jià)格是多少萬(wàn)元？設(shè)今年第一季度每輛車(chē)的銷(xiāo)售價(jià)格為x萬(wàn)元，根據(jù)題意列方程為（　　）

  A． 2000 x + 1 = 2000 （ 1 + 20 % ） x	B． 2000 x + 1 = 2000 （ 1 - 20 % ） x
  C． 2000 x - 1 = 2000 （ 1 + 20 % ） x	D． 2000 x - 1 = 2000 （ 1 - 20 % ） x
  組卷：473引用：3難度：0.9

  解析

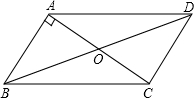• 7．如圖，在平行四邊形ABCD中，AB⊥AC，若AB=8，AC=12，則BD的長(zhǎng)是（　　）

  A．22

  B．16

  C．18

  D．20
  組卷：4187引用：23難度：0.5

  解析

• 8．如圖，在四邊形ABCD中，P是對(duì)角線(xiàn)BD的中點(diǎn)，點(diǎn)E、F分別是AB、CD的中點(diǎn)，AD=BC，∠EPF=140°，則∠EFP的度數(shù)是（　　）

  A．50°

  B．40°

  C．30°

  D．20°
  組卷：5023引用：14難度：0.5

  解析

• 9．若關(guān)于x的分式方程

  1

  x

  -

  2

  +

  k

  x

  +

  2

  =

  6

  x

  2

  -

  4

  有增根x=-2，則k的值為（　　）

  A．- 3 2

  B．- 2 3

  C． 2 3

  D． 3 2
  組卷：1887引用：9難度：0.7

  解析

五、解答題（本大題共三小題，26題8分、26題10分，27題12分，共30分）

• 27．如圖，在平行四邊形ABCD中，CE⊥BC交AD于點(diǎn)E，連接BE，點(diǎn)F是BE上一點(diǎn)，連接CF．
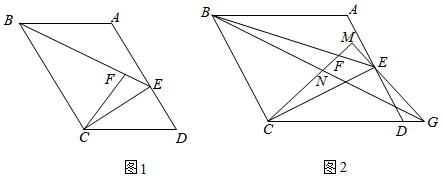
  （1）如圖1，若EC=3DE；BC=BF=4，DC=

  10

  ，求EF的長(zhǎng)．
  （2）如圖2，若BC=EC，連接BE，在BE上取點(diǎn)F，使∠FCD=45°，過(guò)點(diǎn)E作EM⊥CF交CF延長(zhǎng)線(xiàn)于點(diǎn)M，延長(zhǎng)ME、CD相交于點(diǎn)G，連接BG交CM于點(diǎn)N．求證：EG=2MN．
  組卷：542引用：1難度：0.6

  解析

• 28．如圖1，在平面直角坐標(biāo)系xOy中，直線(xiàn)l₂：y=-

  3

  3

  x+

  5

  3

  3

  與x軸交于點(diǎn)B，與直線(xiàn)l₁：y=

  3

  x+b交于點(diǎn)C，C點(diǎn)到x軸的距離CD為2

  3

  ，直線(xiàn)l₁交x軸于點(diǎn)A．
  （1）求直線(xiàn)l₁的函數(shù)表達(dá)式；
  （2）如圖2，y軸上的兩個(gè)動(dòng)點(diǎn)E、F（E點(diǎn)在F點(diǎn)上方）滿(mǎn)足線(xiàn)段EF的長(zhǎng)為

  3

  ，連接CE、AF，當(dāng)線(xiàn)段CE+EF+AF有最小值時(shí)，求出此時(shí)點(diǎn)F的坐標(biāo)以及CE+EF+AF的最小值；
  （3）如圖3，將△ACB繞點(diǎn)B逆時(shí)針?lè)较蛐D(zhuǎn)60°，得到△BGH，使點(diǎn)A與點(diǎn)H對(duì)應(yīng)，點(diǎn)C與點(diǎn)G對(duì)應(yīng)，將△BGH沿著直線(xiàn)BC平移，平移后的三角形為△B′G′H′，點(diǎn)M為直線(xiàn)AC上的動(dòng)點(diǎn)，是否存在分別以C、O、M、G′為頂點(diǎn)的平行四邊形，若存在，請(qǐng)求出M的坐標(biāo)；若不存在，說(shuō)明理由．
  組卷：1030引用：2難度：0.4

  解析