當前位置：試卷中心 > 試卷詳情

2021-2022學年浙江省溫州市十五校聯合體高二（下）期末數學試卷

發布：2024/4/20 14:35:0

1．已知集合P={x|1＜x＜4}，Q={x||x|＜2}，則P∩Q=（　　）
A．{x|1＜x＜2} B．{x|-2＜x＜4} C．{x|2＜x＜4} D．{x|-2＜x＜2}
組卷：95引用：1難度：0.7
解析
2．設
z
=
2
+
i
1
-
i
，則z的共軛復數的虛部為（　　）
A．
3
2
B．
3
2
i
C．
-
3
2
D．
-
3
2
i
組卷：109引用：4難度：0.8
解析
3．已知a,b是實數，則“a|b|＞4”是“a+|b|＞4”的（　　）
A．充分不必要條件 B．必要不充分條件
C．充要條件 D．既不充分也不必要條件
組卷：90引用：1難度：0.7
解析
4．已知
sinα
+
cosα
=
2
3
3
，且
α
∈
（
π
4
，
π
2
）
，則cosα-sinα=（　　）
A．
-
3
3
B．
3
3
C．
6
3
D．
-
6
3
組卷：697引用：1難度：0.7
解析
5．我市某三甲醫院為了響應防疫政策，需要從4名內科醫師和4名外科醫生中派選4名醫生到高速路口進行核酸檢測工作，則派選內科醫生人數不少于外科醫生的概率為（　　）
A．
1
2
B．
17
70
C．
53
70
D．
61
70
組卷：47引用：2難度：0.8
解析
6．函數
f
（
x
）
=
sin
2
x
e
x
-
1
的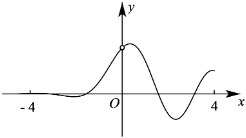圖像大致為（　　）
A． B．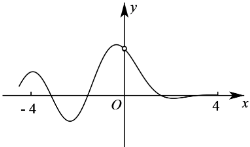
C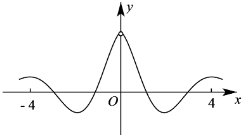． D．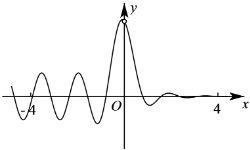
組卷：81引用：2難度：0.8
解析
7．若方程
|
lg
（
x
2
-
2
x
+
3
2
）
|
=
t
有三個不同的實數根x₁，x₂，x₃，則x₁?x₂?x₃=（　　）
A．
-
1
2
B．
1
2
C．1 D．
3
3
2
組卷：89引用：1難度：0.6
解析

21．在矩形ABCD中，AB=2BC，E為線段AB的中點，將△ADE沿直線DE翻折成△A₁DE，M為線段A₁C的中點．
（Ⅰ）求證：BM∥平面A₁DE；
（Ⅱ）當平面A₁DE⊥平面BCD，求平面MDE和平面DEC夾角的余弦值．
組卷：96引用：1難度：0.5
解析
22．已知函數f（x）=a+1-|x-a|，g（x）=ax²-x+1，其中實數a＞0．
（Ⅰ）當x∈[2，4]時，f（x）的最小值為2，求實數a的值；
（Ⅱ）記max{a,b}=
a
,
a
≥
b
b
,
a
＜
b
，設F（x）=max{f（x），g（x）}，若
F
（
x
）
≤
1
2
恒有解，求實數a的取值范圍．
組卷：177引用：2難度：0.5
解析

A．充分不必要條件	B．必要不充分條件
C．充要條件	D．既不充分也不必要條件

A．	B．
C．	D．

1．已知集合P={x|1＜x＜4}，Q={x||x|＜2}，則P∩Q=（ ）