2022-2023學(xué)年山東省德州一中高一（下）月考數(shù)學(xué)試卷（6月份）

一、單項(xiàng)選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求．

• 1．已知向量

  a

  ，

  b

  滿足

  a

  =

  （

  1

  ，

  m

  ）

  ，

  b

  =

  （

  2

  ，-

  1

  ）

  ，且

  （

  2

  a

  +

  b

  ）

  ∥

  b

  ，則m=（　　）

  A．-2

  B． - 1 2

  C． 1 2

  D．2
  組卷：288引用：5難度：0.8

  解析

• 2．若復(fù)數(shù)

  z

  =

  i

  2022

  +

  |

  3

  +

  4

  i

  |

  3

  -

  4

  i

  ，則

  z

  的虛部為（　　）

  A． - 4 5

  B． 4 5

  C． - 2 5 i

  D． 2 5 i
  組卷：56引用：3難度：0.8

  解析

• 3．在△ABC中，內(nèi)角A，B，C所對(duì)的邊分別為a,b,c,△ABC的面積為

  2

  3

  ，

  B

  =

  π

  3

  ，a²+c²=3ac,則b=（　　）

  A． 2 2

  B． 2 3

  C．4

  D． 4 2
  組卷：268引用：3難度：0.8

  解析

• 4．已知l是直線，α、β是兩個(gè)不同平面，下列命題中的真命題是（　　）

  A．若l∥α，l∥β，則α∥β	B．若α⊥β，l∥α，則l⊥β
  C．若l⊥α，l∥β，則α⊥β	D．若l∥α，α∥β，則l∥β
  組卷：273引用：13難度：0.9

  解析

• 5．下列各式化簡(jiǎn)結(jié)果為

  1

  2

  的是（　　）

  A．1-2cos275°

  B．sin15°cos15°

  C．sin14°cos16°+sin76°cos74°

  D．tan20°+tan25°+tan20°tan25°
  組卷：173引用：4難度：0.7

  解析

• 6．如圖所示，在直三棱柱ABC-A₁B₁C₁中，棱柱的側(cè)面均為矩形，AA₁=1，

  AB

  =

  BC

  =

  3

  ，

  cos

  ∠

  ABC

  =

  1

  3

  ，P是A₁B上的一動(dòng)點(diǎn)，則AP+PC₁的最小值為（　　）
  

  A． 3

  B．2

  C． 5

  D． 7
  組卷：255引用：8難度：0.5

  解析

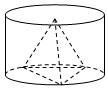• 7．如圖，四面體各個(gè)面都是邊長(zhǎng)為1的正三角形，其三個(gè)頂點(diǎn)在一個(gè)圓柱的下底面圓周上，另一個(gè)頂點(diǎn)是上底面圓心，圓柱的側(cè)面積是（　　）

  A． 2 3 π

  B． 3 2 4 π

  C． 2 2 3 π

  D． 2 2 π
  組卷：292引用：4難度：0.7

  解析

四、解答題：本小題共6小題，共70分。解答應(yīng)寫出文字說明、證明過程或演算步驟．

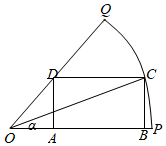• 21．如圖所求扇形OPQ的半徑為1，圓心角為

  π

  3

  ，C是扇形弧上的動(dòng)點(diǎn)，ABCD是扇形的內(nèi)接矩形，記∠COP=α．
  （1）當(dāng)

  AB

  =

  3

  BC

  時(shí)，求tan2α的值；
  （2）記矩形ABCD的面積為f（α），求f（α）最大值，并求此時(shí)α的值．
  組卷：57引用：2難度：0.6

  解析

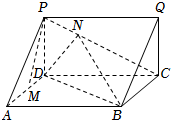• 22．如圖，在三棱柱ADP-BCQ中，側(cè)面ABCD為矩形．
  （1）設(shè)M為AD中點(diǎn)，點(diǎn)N在線段PC上且NC=2PN，求證：PM∥平面BDN；
  （2）若二面角Q-BC-D的大小為θ，

  θ

  ∈

  [

  π

  4

  ，

  5

  π

  6

  ]

  ，且AD=|cosθ|AB，求直線BD和平面QCB所成角的正弦值的取值范圍．
  組卷：140引用：3難度：0.6

  解析