2022年河南省鶴壁市高考數學模擬試卷（理科）（5月份）

一、選擇題（共12小題，每題5分）

• 1．若復數z=1-2i（i為虛數單位）的共軛復數記作

  z

  ，則

  z

  的虛部為（　　）

  A．-2i

  B．2i

  C．2

  D．-2
  組卷：1633引用：3難度：0.9

  解析

• 2．設集合A={x|log₂（x-1）＜2}，B={x|x＜5}，則（　　）

  A．A=B

  B．B?A

  C．A?B

  D．A∩B=?
  組卷：140引用：7難度：0.9

  解析

• 3．若實數x,y滿足約束條件

  2 x + 1 ＞ 0

  x + y ≤ 0

  3 x - y - 3 ≤ 0

  ，則z=5x-y的最大值是（　　）

  A． 9 2

  B．- 9 2

  C．2

  D．-3
  組卷：37引用：6難度：0.7

  解析

• 4．若“?x∈R，ax²-3ax+9≤0”是假命題，則a的取值范圍為（　　）

  A．[0，4]

  B．（0，4）

  C．[0，4）

  D．（0，4]
  組卷：1049引用：6難度：0.8

  解析

• 5．設正項等差數列{a_n}的前n項和為S_n，若S₂₀₁₃=2013，則

  1

  a

  2

  +

  1

  a

  2012

  的最小值為（　　）

  A．1

  B．2

  C．4

  D．8
  組卷：53引用：3難度：0.7

  解析

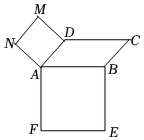• 6．如圖，在同一平面內沿平行四邊形ABCD兩邊AB，AD向外分別作正方形ABEF，ADMN，其中AB=2，AD=1，

  ∠

  BAD

  =

  π

  4

  ，則

  AC

  ?

  FN

  =（　　）

  A． - 2 2

  B． 2 2

  C．0

  D．-1
  組卷：246引用：4難度：0.8

  解析

• 7．將函數y=tan（ωx-

  π

  2

  ）（ω＞0）的圖象分別向左、向右各平移

  π

  6

  個單位長度后，所得的兩個圖象對稱中心重合，則ω的最小值為（　　）

  A． 3 2

  B．2

  C．3

  D．6
  組卷：200引用：3難度：0.6

  解析

選考題：共10分．請考生在第22、23題中任選一題作答．如果多做，則按所做的第一題計分．[選修4—4：坐標系與參數方程]

• 22．在直角坐標系xOy中，曲線C的參數方程為

  x = 3 + 3 sinα + 4 cosα ，

  y = 4 sinα - 3 cosα

  （α為參數），以坐標原點O為極點，x軸的非負半軸為極軸建立極坐標系，直線l的極坐標方程為

  θ

  =

  π

  4

  （

  ρ

  ∈

  R

  ）

  ．
  （1）求曲線C的極坐標方程；
  （2）設直線l與曲線C相交于點A，B，求

  |

  1

  |

  OA

  |

  -

  1

  |

  OB

  |

  |

  ．
  組卷：160引用：3難度：0.7

  解析

[選修4—5：不等式選講]（10分）

• 23．已知函數f（x）=2|x-a|-|x+1|．
  （1）當a=1時，求不等式f（x）≥1的解集；
  （2）若?x∈[-1，1]．使得不等式f（x）≥2x²+x+1成立，求實數a的取值范圍．
  組卷：87引用：4難度：0.6

  解析