2018-2019學(xué)年重慶市九龍坡區(qū)育才中學(xué)九年級（下）開學(xué)數(shù)學(xué)試卷

一、選擇題：（本大題12個小題，每小題4分，共48分）在每個小題的下面，都給出了代號為A、B、C、D的四個答案，其中只有一個是正確的，請將答題卡上題號右側(cè)正確答案所對應(yīng)的方框涂黑．

• 1．下列實(shí)數(shù)中是無理數(shù)的是（　　）

  A． 22 7

  B．π

  C． 9

  D． - 1 3
  組卷：182引用：3難度：0.9

  解析

• 2．如圖圖形中，不是軸對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：56引用：2難度：0.7

  解析

• 3．下列式子運(yùn)算結(jié)果為2a的是（　　）

  A．a(chǎn)?a

  B．2+a

  C．a(chǎn)+a

  D．a(chǎn)3÷a
  組卷：142引用：7難度：0.8

  解析

• 4．使分式

  x

  3

  -

  x

  有意義的x的取值范圍為（　　）

  A．x＞-3

  B．x≠3

  C．x≠-3

  D．x＜3
  組卷：141引用：9難度：0.9

  解析

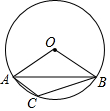• 5．如圖，A，B，C為⊙O上三點(diǎn)，∠AOB=110°，則∠ACB等于（　　）

  A．55°

  B．110°

  C．125°

  D．140°
  組卷：270引用：4難度：0.9

  解析

• 6．已知x,y是方程組

  2 x - y = - 1

  x - 2 y = 4

  的解，則x-y的值是（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：1437引用：3難度：0.8

  解析

• 7．估計(jì)1-

  12

  的值在（　　）

  A．0到-1之間

  B．-1到-2之間

  C．-2到-3之間

  D．-3到-4之間
  組卷：182引用：2難度：0.9

  解析

• 8．下列命題中真命題是（　　）

  A．互補(bǔ)的角一定是鄰補(bǔ)角

  B．三角形的一個外角大于任何一個內(nèi)角

  C．內(nèi)錯角一定相等

  D．同一平面內(nèi)，垂直于同一直線的兩直線平行
  組卷：187引用：5難度：0.9

  解析

四、解答題：（本大題5個小題，第21小題6分，22-25題每小題6分，共46分）解答時每小題必須給出必要的演算過程或推理步驟，請將解答書寫在答題卡（卷）中對應(yīng)的位置上．

• 25．請閱讀下列材料：
  問題：已知方程x²+x-1=0，求一個一元二次方程，使它的根分別是已知方程根的2倍．
  解：設(shè)所求方程的根為y,則y=2x所以x=

  y

  2

  ．
  把x=

  y

  2

  代入已知方程，得（

  y

  2

  ）²+

  y

  2

  -1=0
  化簡，得y²+2y-4=0
  故所求方程為y²+2y-4=0．
  這種利用方程根的代換求新方程的方法，我們稱為“換根法”．
  請用閱讀材料提供的“換根法”求新方程（要求：把所求方程化為一般形式）：
  （1）已知方程x²+x-2=0，求一個一元二次方程，使它的根分別為已知方程根的相反數(shù)，則所求方程為：

  ；
  （2）已知關(guān)于x的一元二次方程ax²+bx+c=0有兩個不等于零的實(shí)數(shù)根，求一個一元二次方程，使它的根分別是已知方程根的倒數(shù)．
  組卷：2136引用：22難度：0.5

  解析

五、解答題：（本大題1個小題，共12分）解答時每小題必須給出必要的演算過程或推理步驟，請將解答過程書寫在答題卡中對應(yīng)的位置上．

• 26．如圖1，拋物線y=-

  1

  3

  x

  2

  -

  2

  3

  3

  x+3與x軸交于A、B兩點(diǎn)，與y軸交于點(diǎn)C，連接AC、BC．
  （1）求線段AC的長；
  （2）如圖2，E為拋物線的頂點(diǎn)，F(xiàn)為AC上方的拋物線上一動點(diǎn)，M、N為直線AC上的兩動點(diǎn)（M在N的左側(cè)），且MN=4，作FP⊥AC于點(diǎn)P，F(xiàn)Q∥y軸交AC于點(diǎn)Q．當(dāng)△FPQ的面積最大時，連接EF、EN、FM，求四邊形ENMF周長的最小值．
  （3）如圖3，將△BCO沿x軸負(fù)方向平移

  3

  個單位后得△B'C'O'，再將△B'C'O'繞點(diǎn)O'順時針旋轉(zhuǎn)α度，得到△B″C″O'（其中0°＜α＜180°），旋轉(zhuǎn)過程中直線B″C″與直線AC交于點(diǎn)G，與x軸交于點(diǎn)H，當(dāng)△AGH是等腰三角形時，求α的度數(shù)．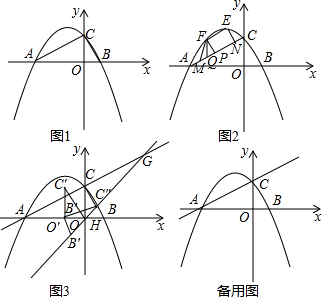
  
  組卷：256引用：2難度：0.1

  解析