當前位置：試卷中心 > 試卷詳情

2009-2010學年重慶十一中高一（上）數學單元測試（11）（函數與數列）

發布：2024/12/21 19:30:2

1．滿足{2}?M?{1，2，3}的集合M有（　　）
A．2個 B．3個 C．4個 D．5個
組卷：134引用：2難度：0.9
解析
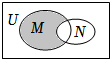2．如圖，U為全集，M，N是集合U的子集，則陰影部分所表示的集合是（　　）
A．M∩N B．?_U（M∩N） C．（?_UM）∩N D．（?_UN）∩M
組卷：51引用：3難度：0.9
解析
3．函數y=5^x+1（x∈R）的反函數是（　　）
A．y=log₅x+1（x＞0） B．y=log₅（x+1）（x＞-1）
C．y=log₅x-1（x＞0） D．y=log₅（x-1）（x＞1）
組卷：51引用：1難度：0.9
解析
4．若x,a,2x,b成等比數列，則
a
b
的值為（　　）
A．
1
2
B．
2
C．2 D．
2
2
組卷：50引用：1難度：0.9
解析
5．函數
y
=
lo
g
1
2
（
-
x
2
+
6
x
-
8
）
的單調遞減區間為（　　）
A．[3，4） B．（2，3] C．[3，+∞） D．[2，3]
組卷：241引用：1難度：0.9
解析
6．若p是真命題，q是假命題，則①p且q；②p或q；③非p；④非q.四個命題中假命題的個數是（　　）
A．1 B．2 C．3 D．4
組卷：25引用：1難度：0.7
解析
7．已知等比數列{a_n}的公比為
-
1
4
，則
a
1
+
a
3
+
a
5
+
…
+
a
2
n
-
1
a
3
+
a
5
+
a
7
+
…
+
a
2
n
+
1
=（　　）
A．
-
1
16
B．16 C．
1
2
D．2
組卷：59引用：1難度：0.9
解析

A．y=log₅x+1（x＞0）	B．y=log₅（x+1）（x＞-1）
C．y=log₅x-1（x＞0）	D．y=log₅（x-1）（x＞1）

1．滿足{2}?M?{1，2，3}的集合M有（ ）